「命題の逆・裏・対偶」とは?意味と真偽についてわかりやすく解説
高校数学Ⅰで学習する論証について、「命題の逆」「命題の裏」「命題の対偶」とはどういうものかをわかりやすく解説するよ。
命題の逆・裏・対偶は元の命題が真のとき、真と偽のどちらになるのか、くわしい例を紹介しながら説明するよ。
論証:命題の逆・裏・対偶(たいぐう)とは?
今回の内容「命題の逆・裏・対偶(たいぐう)」も、前回の「命題と条件」のところで話したのと同じように、論理的に話を組み立て、考え、表現するために必要な事なんだ。
そして、論理的に話を組み立て、考え、表現することを、「論証」と言うんだよ。
具体的には、これから「直接証明するのは難しい事を証明しやすくする論証の方法」を2つ紹介するんだけど、今日はそのために必要な言葉を学んでいくよ。
この単元も、「初めて学ぶ人」と「もっと先の数学を勉強していて、この単元の復習をする人」で、読んでほしい内容を分けて説明するよ。
「復習する人」のための内容は、四角で囲っておくから参考にしてね!
命題の逆・裏・対偶とは?
命題の逆・裏・対偶
教科書の説明
命題「\(p \Rightarrow q\)」と関連する命題を考えると、
命題「\(q \Rightarrow p\)」を命題「\(p \Rightarrow q\)」の逆
命題「 \(\overline{ p } \Rightarrow \overline{ q }\) 」を命題「\(p \Rightarrow q\)」の裏
命題「 \(\overline{ q } \Rightarrow \overline{ p }\) 」を命題「\(p \Rightarrow q\)」の対偶
という。
ある命題が真であっても、その命題の逆は真とは限らない。また、裏も真とは限らない。
命題「\(p \Rightarrow q\)」とその対偶「\(\overline{ q } \Rightarrow \overline{ p }\)」とは、真偽が一致する。
「逆」や「裏」は日常生活でも使う言葉だけど、「対偶(たいぐう)」というのは初めて聞いた言葉だよね。 図にすると、こうなるんだ。
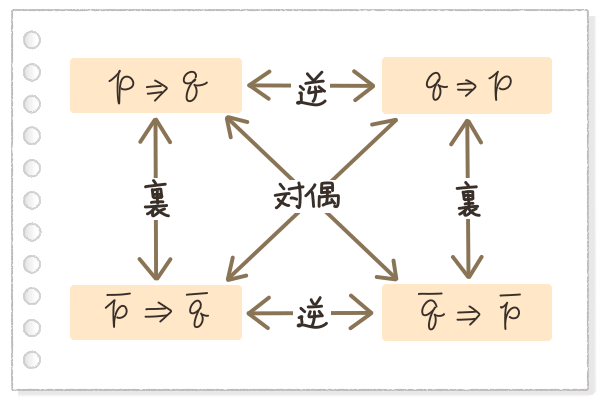
これが「命題の逆・裏・対偶」の関係を図にしたものだよ。
この図の中の斜めの矢印で書かれている「対偶」という関係が、命題を証明するときに強力なパワーを発揮してくれるんだ!
今日は、この「対偶」を作れるようになって、そして「対偶」が持つ重要な鍵を理解するのが目標なんだ。
そのために、言葉をひとつずつ攻略していこう。
今日は、この2つの例を使って説明していくよ。
例1:「カラス⇒黒い」
例2:「4の倍数⇒2の倍数」
例1は、逆・裏・対偶を作ったときに、文章としてどんなふうになるかイメージしてもらうための例なんだ。
今回の説明では「カラスは必ず黒い」ということにしているよ。実際には他の色のカラスもいるかもしれないけど、ここでは「カラスは黒い」として読んでほしいんだ。
例2は、数学的な内容の代表として使っていくよ。
早速、この2つの命題の真偽を確認しておこう。
例1:「カラス⇒黒い」
カラスは必ず黒い。この命題は真である。
さっき言った通り、今回の説明ではカラスの色は黒としているので、例1の命題は真だと言えるね。
例2:「4の倍数⇒2の倍数」
そもそも4が2の倍数なので、その4を何倍かして作った4の倍数は当然2の倍数でもある。
この命題は真である。
例2も真だという事が分かったね。
それでは、「逆・裏・対偶」をひとつずつ攻略していこう!
命題の逆とは?
命題「\(p \Rightarrow q\)」の逆は、「\(q \Rightarrow p\)」
pとqの位置が逆になっているのが分かるかな?
言葉の通り、pとqの位置を逆にしたものが、命題の「逆」なんだ。
例1:「カラス⇒黒い」の逆は「黒い⇒カラス」
例2:「4の倍数⇒2の倍数」の逆は「2の倍数⇒4の倍数」
単純に、仮定と結論を逆にすると「逆」が作れるんだね
その通り!仮定と結論という言葉も、大切な言葉だったね。
ここで注目してほしいのは、作った「逆」が真か?偽か?ってことなんだ。
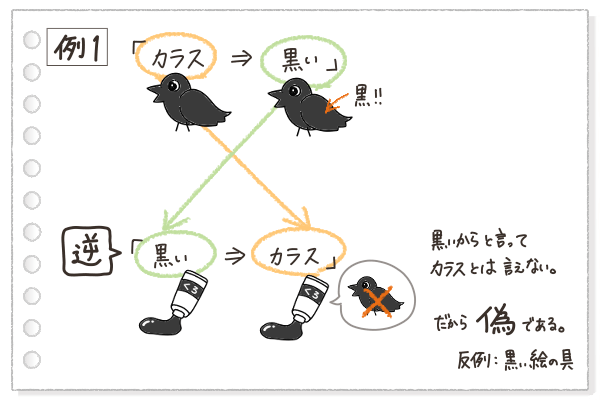
例1では、「逆」の文章は、「黒いならば、カラスだ」となるけれど、黒いものはカラス以外にもたくさんあるよね。
例えば「黒い絵の具」は、黒いけれどもカラスではない。
つまり、「黒い絵の具」という反例があるから、例1の「逆」は偽ってことになるね。
例2についても見てみよう。
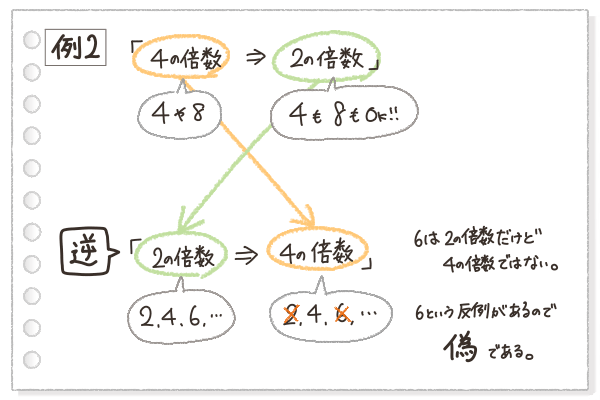
例2では、「逆」の命題「2の倍数ならば、4の倍数」に対して、6という反例があげられるね。
6は2の倍数だけれども、4の倍数ではないからね。
ってことで、例2の「逆」も、偽だと分かった。
例1と例2の結果から、元の命題が真であっても、その「逆」は真であるとは限らない、ということが分かったかな?
まずは「逆」を作れるようになることが第一歩だね。そして「逆」を作れたら、その真偽をチェックできるようになろう!
元の命題が真のとき、「逆」が真になる場合もあるよ!
例3:もとの命題「偶数⇒2の倍数」について、その逆は「2の倍数⇒偶数」
この例3場合は、元の命題が真で、その「逆」も真になっているでしょ?
さて、気づいたかな?
これは、前回の「命題と条件」のところで、「同値」の説明をしたときと同じ例なんだ!
※同値(どうち)とは、値(あたい)が同じこと。
偶数とは「2で割り切れる数」だから、「偶数」と「2の倍数」は同値だよ。
つまり、命題「\(p \Rightarrow q\)」において、pとqが同値ならば、その逆も真になるんだよ。
命題の裏とは?
命題「\(p \Rightarrow q\)」の裏は、「 \(\overline{ p } \Rightarrow \overline{ q }\) 」
「 \(\overline{ p }\) 」という記号を覚えているかな?
「 \(\overline{ p }\) 」というのは、「pではない」という意味だったね。ちなみに、読み方は「pバー」だったよ。
つまり、「裏」は、pとqの順番はそのままなんだけど、内容を「pではない」と「qではない」に変えるってことだね。
例1と例2の「裏」を作ってみると、こうなるよ。
例1:「カラス⇒黒い」の裏は「カラスじゃない⇒黒じゃない」
例2:「4の倍数⇒2の倍数」の裏は「4の倍数じゃない⇒2の倍数じゃない」
「裏」は、仮定と結論が言っていることを、それぞれ裏返しにして作るイメージだね。
そうだね!
順番は変わらずに、内容が裏返っているイメージを持つといいよ!
次に、この「裏」の真偽がどうなっているか確認してみよう。
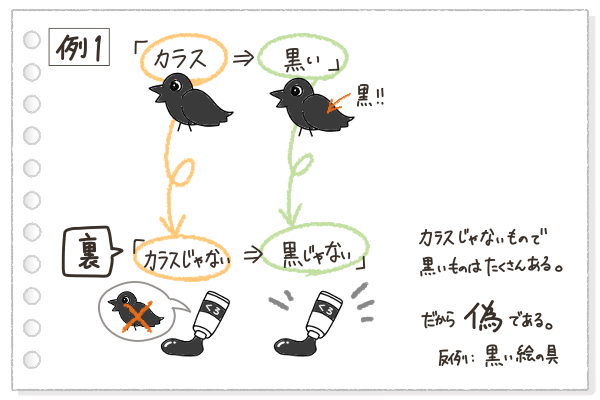
例1では、「裏」の文章は「カラスじゃないならば、黒じゃない」となるけれど、カラスじゃなくても、黒いものはたくさんあるよね。
例えば「黒い絵の具」は、カラスじゃないもので、黒いものだといえる。
つまり、「黒い絵の具」という反例があるから、例1の「裏」は偽ってことになるね。
例2についても見てみよう。
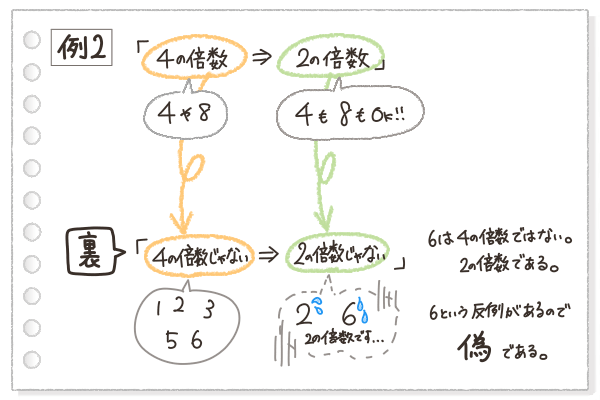
例2では、「裏」の命題「4の倍数ではないならば、2の倍数ではない」に対して、6という反例があげられるね。
6は4の倍数じゃないけれど、2の倍数だよね。
ってことで、例2の「裏」も、偽だと分かった。
例1と例2の結果から、元の命題が真であっても、その「裏」は真であるとは限らない、ということが分かったね。
同値の場合はどうなるのかを確認しておこう。
例3:もとの命題「偶数⇒2の倍数」について、その裏は「偶数ではない⇒2の倍数ではない」
つまり、「奇数⇒2の倍数ではない」
「偶数と奇数」のように、片方であることを否定すると、全部もう片方になるようなときは、「偶数ではない」をもう一歩踏み込んで「奇数である」と書くよ。
そして、例3も、元の命題もその「裏」も、両方真だったね。
つまり、「逆」のときと同じように、命題「\(p \Rightarrow q\)」において、pとqが同値ならば、その裏も真になるんだよ。
命題の対偶とは?
命題「\(p \Rightarrow q\)」の対偶は、「\(\overline{ q } \Rightarrow \overline{ p }\) 」
いよいよ対偶の説明だね。
対偶を作る時は、2つのステップで作るといいよ。
①元の命題の「裏」を作る
②作った「裏」を「逆」にする
具体的にやってみよう!
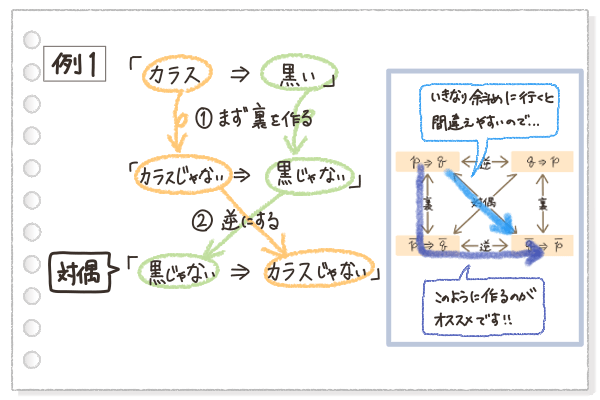
「逆」と「裏」を作る作業を両方すればいいんだね!ということは、先に「逆」をしてから「裏」をしてもいいの?
いいところに気が付いたね!
その通り、「逆」と「裏」を作る作業を両方行えばいいんだよ。
順番はどちらが先でも大丈夫だから、自分が考えやすい方で作るといいよ! それでは、作った「対偶」が真か偽かを確認してみようか。
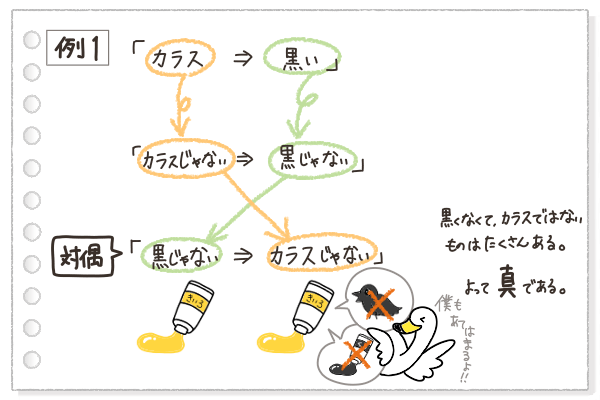
例1では、「対偶」の文章は「黒じゃないならば、カラスじゃない」となるね。黒くないもので、カラスでもないものはたくさんあるよね。
黄色い絵の具もそうだし、白鳥もあてはまるよね!
そして、今日の説明ではカラスは必ず黒いってことになっているので、黒くないならカラスではないと分かる。
つまり、例1の「対偶」は真だと言えるんだ。
例2についても見てみよう。
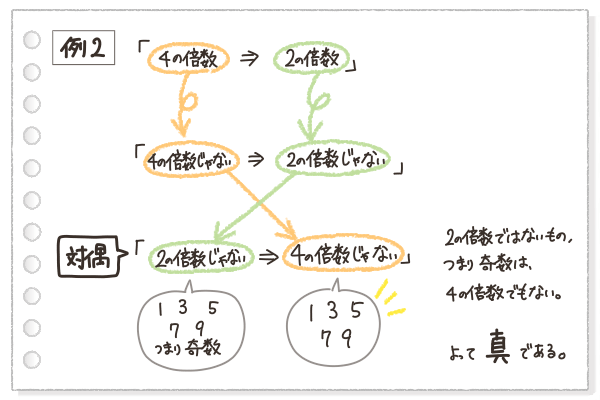
例2では、「対偶」の命題は「2の倍数でないならば、4の倍数ではない」となるね。
2の倍数ではないっていうことは、奇数だと言えるよね。
奇数はもちろん4の倍数ではない。だから「対偶」の文章「2の倍数でないならば、4の倍数ではない」は当然のことだ!といえる。
例2の「対偶」も、真だと言えたよ。
同値の場合も、対偶は真になるよ。
例3:もとの命題「偶数⇒2の倍数」について、その対偶は「2の倍数ではない⇒偶数ではない」
つまり、「2の倍数ではない⇒奇数」
例3の元の命題もその「裏」も、両方真だよね。
つまり、命題「\(p \Rightarrow q\)」において、pとqが同値ならば、その対偶も真になるってことだ。
ここまでを振り返ると…「逆」と「裏」は偽になって、「対偶」だけは真になる、ってことかな?
そうだね、それは正解ではあるんだけど、完全な正解とは言えないんだ。
もとの命題が真のとき、
- 「逆」と「裏」は、真になるとは限らない(つまり、偽になるかもしれない)
- 「対偶」は必ず真になる
これが完全な正解で、何より重要なのは、もとの命題の真偽と、対偶の真偽は一致するということなんだ!
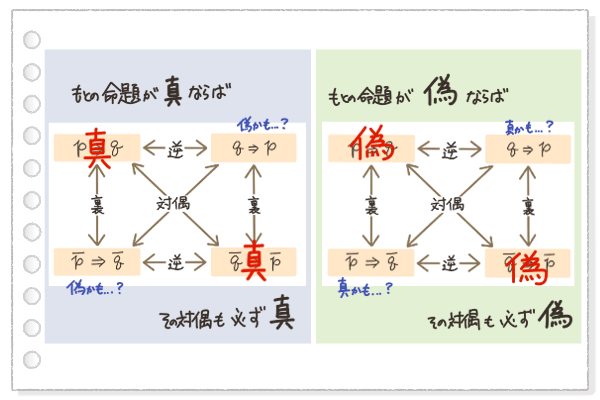
もとの命題が真ならば、その対偶は必ず真になるし、
元の命題が偽ならば、その対偶も必ず偽になるんだよ。
さっきの図の右側のように、もとの命題が偽の時、対偶がどうなるかを確かめておこう。
まず、真偽を確かめてみると偽になる、例4を用意するね。
例4:「\(\begin{eqnarray}x^2=9\end{eqnarray}\) ⇒\(\begin{eqnarray}x=3\end{eqnarray}\)」
\(\begin{eqnarray}x^2=9\end{eqnarray}\)を解くと、\(\begin{eqnarray}x=\pm 3\end{eqnarray}\) だから、
\(\begin{eqnarray}x=- 3\end{eqnarray}\) という反例があるため、この命題は偽である。
では、例4の「対偶」を作ってみよう。
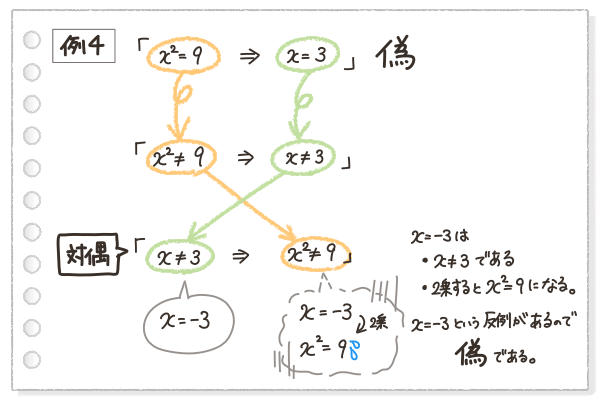
例4では、「対偶」に対して、\(\begin{eqnarray}x=- 3\end{eqnarray}\) という反例があげられるね。
\(\begin{eqnarray}x=- 3\end{eqnarray}\) は、仮定である \(\begin{eqnarray}x \neq 3\end{eqnarray}\) を満たしていて、2乗すると \(\begin{eqnarray}x^2=9\end{eqnarray}\)となるから、結論である \(\begin{eqnarray}x^2 \neq 9\end{eqnarray}\)を満たさない。
これで、もとの命題が偽であった例4では、その「対偶」も、偽だと分かったね。
命題の逆・裏・対偶 まとめ
「命題の逆・裏・対偶」について、今回学習したことをまとめたよ。
命題「\(p \Rightarrow q\)」の「逆」とは
- pとqの位置を逆にした、「\(q \Rightarrow p\)」がこの命題の「逆」
- もとの命題「\(p \Rightarrow q\)」が真であっても、その「逆」が真になるとは限らない
命題「\(p \Rightarrow q\)」の「裏」とは
- 条件pを否定した と、条件qを否定した を考えて作る「 ⇒ 」がこの命題の「裏」
- 「pではない」と、pの内容を裏返しにしているイメージで覚えると良い
- もとの命題「\(p \Rightarrow q\)」が真であっても、その「裏」が真になるとは限らない
命題「\(p \Rightarrow q\)」の「対偶」とは
- ①まず、「裏」を作る
②それを逆にする
という順番で作ると良い - 「pではないならば、qではない」という文章になる
- もとの命題「\(p \Rightarrow q\)」と、その対偶「 \(\overline{ q } \Rightarrow \overline{ p }\) 」の真偽は一致する。
つまり、もとの命題が真であれば、その対偶も真となり、
もとの命題が偽であれば、その対偶も偽となる。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



