「対偶を利用した証明」とは?証明の書き方と例をわかりやすく解説
「対偶」って何のために作るの?どんな時に便利なの? 「対偶を利用した証明」をどんな時に使うのか、どうして便利なのかをわかりやすく解説。証明の書き方についてもくわしく解説していくよ。
論証:対偶を利用した証明
今回の内容「対偶を利用した証明」では、いよいよ論理的に話を組み立て、考え、表現する「論証」を実践していくよ。 具体的には、「論証」の単元で2つ紹介する「直接証明するのは難しい事を証明しやすくする論証の方法」のうちの1つめが、この「対偶を利用した証明」なんだ。
ひとことアドバイス
実は、数学Ⅰで習う時の「対偶を利用した証明」の問題は似ている問題が多いんだ。
これまでに聞いたことのない「対偶」なんていう言葉が出てくるから、すごく難しそう…っていうイメージを持ってしまう人が多いんだけど、この単元を習った時の定期テストでは似たパターンの問題が出ることが多いから、授業で習った問題と、今から説明する問題を見比べて、どこが似ていてどこが違うかを見つけてみてね。 テスト対策にもきっと役立つよ!
「対偶」を利用するのはなぜ?
ある命題を証明するために、その対偶を考えて証明することがある
前回、対偶とは何かについて学んだときに、
「 もとの命題の真偽と、対偶の真偽は一致する」
という事が大事だよって言ったのを覚えているかな?
実はこのことが「直接証明するのは難しい事」を証明する時に強力なパワーを発揮するんだ! この、例1を考えてみよう。
例1
整数nについて、3n+5が偶数ならば、nは奇数であることを証明せよ。
どうだろう、まず何をすればいいか、思いつくかな?
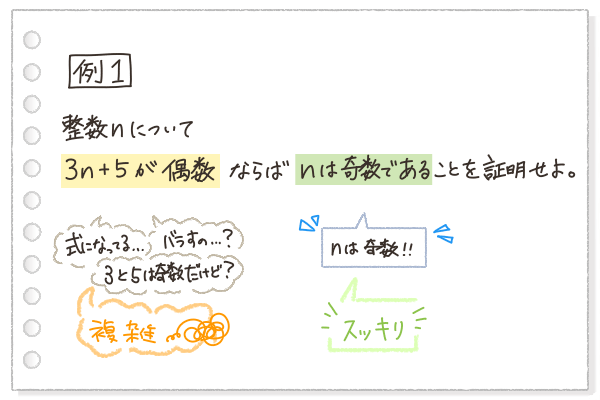
3n+5って、式になっている・・・?じゃあ、式を分解する?
この「式」は偶数と言っているけど、3と5は奇数だし、どうしよう?
・・・ということで、何から始めていいか思いつかないよね。
例1を見てまず困るのは、前の部分(仮定)が複雑で、何から始めればいいか分からないということだよね。
でも、後ろの部分(結論)の方はスッキリしている。 実は、例1のような、
前の部分(仮定)←複雑
↓
後ろの部分(結論)←スッキリ
という形の命題を証明するときに、対偶がパワーを発揮するんだ!
例1の対偶を作ってみるよ
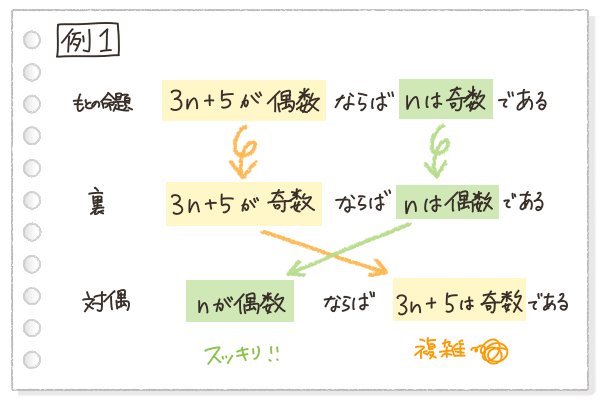
対偶を作ると、前の部分(仮定)と後ろの部分(結論)がひっくり返ったでしょ?
これで、スッキリしている「nが偶数」ということから証明が始められるんだ。
太郎「でも、ひっくり返すだけなら「逆」を作るだけでいいんじゃないの?」
そうだね、ひっくり返すだけなら「逆」で良さそうなんだけど、もとの命題が真でも「逆」は偽になっちゃう時があったよね。
でも、もとの命題が真ならば「対偶」も必ず真になるんだ。
つまり、対偶が正しいと言えれば、もとの証明したかったことも正しいと言えるわけだ。
最初に言った、
もとの命題の真偽と、対偶の真偽は一致する
このことが、強力なパワーを発揮しているんだよ。
真偽が変わってしまうかもしれない「逆」ではなくて、「対偶」を使うのは、もとが真なら必ず対偶も真になるからなんだね
対偶を利用するのはなぜ?
- 前の部分(仮定)が複雑、後ろの部分(結論)がスッキリしている時には、対偶を作るとスッキリしている方から証明が始められるから。
- 対偶が正しいと言えれば、もとの証明したかったことも正しいと言えるから。
対偶を利用した証明(形の確認)
それでは、実際に証明してみよう。
まずは、対偶を利用した証明がどんな形で書かれるかを確認していくよ。 対偶の証明は、こういう形で書くんだ。
対偶を書く
↓
証明の本文(計算式など)を書く
↓
対偶が真なら、もとの命題も真であると宣言する
では、例1にとりかかろうか。
例1
整数nについて、3n+5が偶数ならば、nは奇数であることを証明せよ
証明の内容の詳しい解説は後の「証明の本文の解説」セクションで行うよ。 ここではまず、「対偶を利用した証明」がどんな形で書かれているかに注目してほしいんだ。
| 証明の形(書く内容) | 証明の形(流れ)の解説 |
|---|---|
| 証明 | 「証明」を書いて、証明が始まることを宣言。 |
| この命題の対偶は,「nが偶数ならば,3n+5は奇数である」である。 | もとの命題の対偶を書く。 |
| nを偶数とすると,ある整数kを用いてn=2kと表される。 よって 3n+5=3・2k+5 =6k+5 =2・3k+4+1 =2(3k+2)+1 ここで,3k+2は整数であるから,3n+5は奇数である。 | ここが本文。 |
| したがって,対偶が真であるから,もとの命題も真である。 | 対偶が真なら元の命題(問題文)も真であることを宣言して、 |
| 証明終 | 「証明終」を書いて終了。 |
大まかな形として、
対偶を書く
↓
証明の本文(計算式など)を書く
↓
対偶が真なら、もとの命題も真であると宣言する
となっていることはわかったかな? 次のセクションで、対偶を利用した証明の書き方のルールについて、さらに詳しく解説するよ。
対偶を利用した証明(書き方のルール)
対偶を利用した証明の書き方のルールについてまとめておくよ。
| 準備 | 確認 | 「前の部分(仮定)⇒後ろの部分(結論)」 複雑 スッキリ という形であることを確認 |
| 対偶作成 | 対偶を作る | |
| 証明 | ①対偶を書く | 証明の最初に この命題の対偶は,「〇〇ならば,△△である」である。 という文章を書く |
| ②本文 | 証明の本文を書く | |
| ③締めの宣言 | 証明の最後に したがって,対偶は真であるから,もとの命題も真である。 という文章を書く |
対偶を利用できると判断したら、まずは慎重に「対偶」を作ろう。
証明を書き始めたら、「①対偶を書く」の文章を書くことで「これから、この対偶を証明しますよ」と宣言するんだ。
そして、②本文を書いたら、最後に「③締めの宣言」の文章を忘れずに書こう。
この文章がないと、もとの命題(問題として証明すべき内容)が証明されたとは言えなくなっちゃうから、要注意だよ。 例2を証明しながら、書き方のルールを整理しておこう。
例2
整数nについて、n2が偶数ならば,nは偶数であることを証明せよ
まずは準備だね。
「複雑⇒スッキリ」になっているかを確認。
整数nについて、n2が偶数ならば,nは偶数であることを証明せよ
n2が偶数 は、「nが2乗」になっているので、複雑だね。
nは偶数 はスッキリだね。
対偶を利用できそうだと確認できたね。
次は、対偶を作ろう。
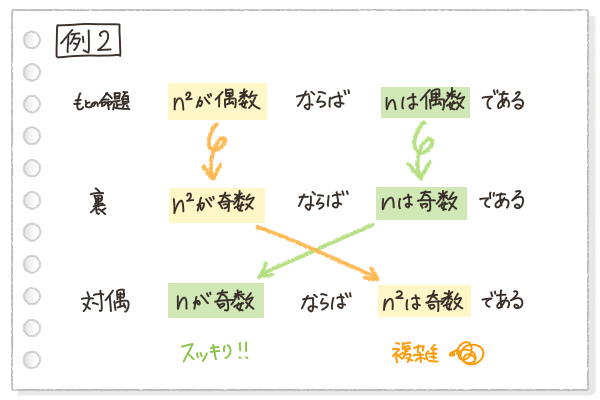
では、証明を書いていくよ。
| ①対偶を書く | 証明 この命題の対偶は,「nが奇数ならば,n2は奇数である」である。 |
| ②本文 | nを奇数とすると,ある整数kを用いてn=2k+1と表される。 よって n2=(2k+1)2 =4k2+4k+1 =2(2k2+2k)+1 ここで,2k2+2kは整数であるから,n2は奇数である。 |
| ③締めの宣言 | したがって,対偶が真であるから,もとの命題も真である。 証明終 |
証明の書き方のルールはわかったかな? 他の問題でも、対偶を利用した証明の書き方のルールは同じなので、参考にしてみてね。
証明本文の解説のための準備(整数の表し方)
対偶を利用した証明の「形」がわかったところで、本文の解説をするよ。
ここで、今回の「対偶を利用した証明」でも、次の「背理法」でも、そしてこの単元以外でも、これから先よく使うことになる「整数の表し方」を、偶数・奇数・○○の倍数について解説するね。
偶数の表し方
まずは偶数をどう表すか考えてみるよ。
偶数って、
「偶数」=「2の倍数」=「2×(何か)」 と言えるよね?
このことを使って、証明の中で「偶数」を使う時には、
nが偶数である時,ある整数kを用いてn=2kと表す。
というふうに書くんだ
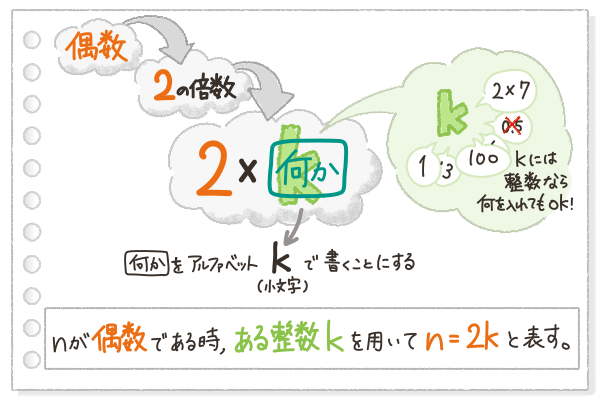
2×(何か)の「何か」を、アルファベットのkで書いている、っていうことだね。
この時使うアルファベットは、問題文や証明の文章で既に使われている文字(今の場合は、nのこと)以外なら何を使ってもいいんだけど、数学ではこういう時、kを使うことが多いんだよ。
奇数の表し方
偶数を2kと表すことが分かると、奇数も簡単に作れるんだ。
整数を並べると、偶数と奇数は順番に出てくるよね。
「偶数の次は奇数になる」=「2kの次は奇数」=「2k+1は奇数」 ってことで、奇数は2k+1で表すことが出来るよ!
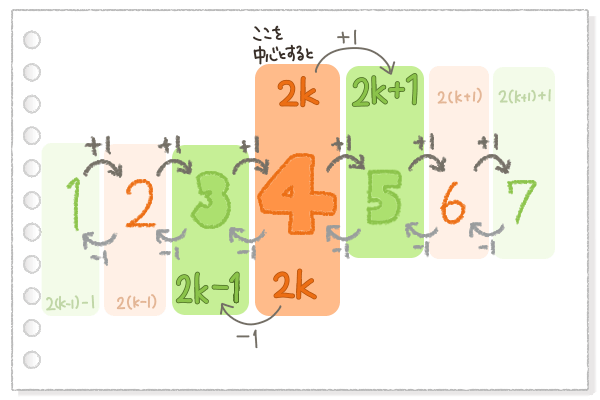
この図からも分かるように、奇数は2k-1で表してもいいんだ。
その時扱っている式の形や、証明したい内容によって、2k+1か2k-1のうち、使いやすい方を使っていいんだよ。
ちゃんと文章にすると、こんな感じ。
nが奇数である時,ある整数kを用いてn=2k+1と表す。
または、 nが奇数である時,ある整数kを用いてn=2k-1と表す。
是非覚えておいてね!
〇〇の倍数
偶数、つまり2の倍数を2kと書く考え方を使うと、3の倍数や7の倍数といった「〇〇の倍数」も表すことが出来るよ。
例えば、3の倍数なら、
3の倍数=3×(何か) ってことだよね。
だから、
nが3の倍数である時,ある整数kを用いてn=3kと表す。
というふうに書けるんだ。
今紹介した、偶数・奇数・○○の倍数の書き方は、整数を扱う時によくので、是非感覚をつかんでおいてほしいな!
kは小文字じゃないといけないの?
ひとことアドバイス
そうだね、自分が「ある整数を『これ』にします」と宣言すれば、どんな文字でも、記号でも、なんなら絵でもいいんだ。
もっと数学を学んでいくとギリシャ文字なんかも使うことになるんだけど、基本的には英語のアルファベットを使うことが多いんだよ。論文として発表したり本にしたりするときには英語で印刷することが多いから、世界中で使われている文字にしておく方が便利なんだ。
その前提で、アルファベットの各文字には既に役割があるものがあるんだよ。
例えば、xは未知の数「未知数」だし、nはnatureの頭文字で「自然数」を表すという役割がある。
そして、大文字には「その種類のもの全部」という役割があるんだ。
nは小文字だと「ひとつの自然数」だけど、Nとすると自然数全体を表す文字として使われることが多いんだ。 ひとつの整数を表すときに小文字のkにするのは、「自然数などの特別なものではない、ひとつの整数」を表すからなんだよ。
選ばれる文字にもちゃんと意味があるんだね!!
証明本文の説明
それでは、今回解いてきた例1と例2の証明の詳しい解説をするよ。
まずは例1から。
例1
整数nについて、3n+5が偶数ならば、nは奇数であることを証明せよ
| 書く内容 | 詳しい解説(注意点は赤い文字) |
|---|---|
| 証明 | 「証明」を書いて、ここから証明が始まることを宣言。 |
| この命題の対偶は,「nが偶数ならば,3n+5は奇数である」である。 | もとの命題の対偶を書く。 |
| nを偶数とすると,ある整数kを用いてn=2kと表される。 | 「nが偶数」であることから始めるんだけど、偶数を表すためのkは勝手に持ってきた文字なので、必ず「kがどんな数字なのか」を書かないといけないんだ。 今回は「ある整数k」と説明しているね。 kは整数ならばどんな数字でもいいですよ、ということだね。 |
| よって 3n+5=3・2k+5 ☆ =6k+5 ★ =6k+4+1 ♪ =2(3k+2)+1 ◇ | 3n+5が奇数になることを、計算して示していくよ。 さっき紹介した通り、奇数になることを言うには式が 2×(何か)+1 の形になることを言えればOKなんだ。 計算して出てきた6k+5を、できるだけ2でくくって、 2×(何か)+1 の形を作るのが目標。 ♪ 6kはそのままで2でくくれるよね。 5は4+1って分解して、4だけ2でくくれるようにして、 1は何もせず置いておくんだ。 ◇ 2でくくれるところは全部2でくくって、 2×(何か)+1 の形の完成だね。 |
| ここで,3k+2は整数であるから,3n+5は奇数である。 | 奇数は2×(何か)+1の形になれば、(何か)の部分はどんなに複雑な式になっても構わないんだけど、整数でないといけないんだ。 分数や小数だと2が約分されちゃったりするからね。 もともとkは整数なので、3k+2ももちろん整数。 これは絶対に確認しないといけないので、忘れずに書こう。 |
| したがって,対偶が真であるから,もとの命題も真である。 | 対偶が真なら元の命題(問題文)も真であることを宣言して、 |
| 証明終 | 証明終を書いて終了。 |
続いて、例2の解説だよ。
例2
整数nについてn2が偶数ならば,nは偶数であることを証明せよ
| 書く内容 | 詳しい解説(注意点は赤い文字) |
|---|---|
| 証明 | 「証明」を書いて、ここから証明が始まることを宣言。 |
| この命題の対偶は,「nが奇数ならば,n2は奇数である」である。 | もとの命題の対偶を書く。 |
| nを奇数とすると,ある整数kを用いてn=2k+1と表される。 | 「nが奇数」であることから始めるんだけど、例1と同じように、kの説明を忘れないようにね! |
| よって n2=(2k+1)2 ☆ =4k2+4k+1 ★ =2(2k2+2k)+1 ♪ | n2が奇数になることを、計算して示していくよ。 例1と同じく、奇数になることを言うには式が 2×(何か)+1 の形になることを言えればOKだよ。 計算して出てきたを、4k2+4k+1をできるだけ2でくくって、 2×(何か)+1 の形を作んだ。 ♪ 4k2+4kは2でくくれるよね。 1はそのまま置いておくんだ。 2×(何か)+1 の形が完成! |
| ここで,2k2+2kは整数であるから,n2は奇数である。 | 例1のときも説明した通り、奇数は2×(何か)+1の形になれば、(何か)の部分がどんなに複雑な式になっても構わないけど、整数でないといけなかったよね。 もともとkは整数なので、2k2+2kも整数だ。 この確認、書き忘れないように気を付けて! |
| したがって,対偶が真であるから,もとの命題も真である。 | 対偶が真なら元の命題(問題文)も真であることを宣言して、 |
| 証明終 | 証明終を書いて終了。 |
例1と例2には、似ているところがたくさんあったね! どこが似ていて、どこが違ったかを分析するのもとてもいい勉強法なので、是非分析してみてね。
「対偶を利用した証明」まとめ
「対偶を利用した証明」について、今回学習したことをまとめたよ。
対偶を利用するのはなぜ?
- 前の部分(仮定)が複雑、後ろの部分(結論)がスッキリしている時には、対偶を作ると前後が反対になって、スッキリしている方から証明が始められるから。
- 対偶が正しいと言えれば、もとの証明したかったことも正しいと言えるから。
「対偶を利用した証明」の書き方のルール
- 準備で2つ、証明で3つの手順がある
準備① 「前の部分(仮定)が複雑、後ろの部分(結論)がスッキリ」という形であることを確認
準備② 対偶を作る
証明① 「対偶」を書く
証明② 証明の本文(計算式など)を書く
証明③ 対偶が真なら、もとの命題も真であると宣言する
数学Ⅰで学ぶ「対偶を利用した証明」では似た問題が多いので、このルールを真似て書く練習をしておくとよい。
整数の表し方
- nが偶数 → n=2k
- nが奇数 → n=2k+1
- nが3の倍数 → n=3k
証明の中でこの書き方使う時は、必ずkの説明をする。説明の文章は「kを整数とする」など。 (問題によって、整数ではなく自然数、正の整数などの言葉が変わる時もある)
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。




ものすごく分かりやすくて感動しました。ありがとうございます。