「整式の乗法」「指数法則」をわかりやすく解説
「整式の乗法」と「指数法則」
教科書にはなんて書いてあるの??
「aをn個掛けた累乗」を\(a^n\)(aのn乗)と書き、nは指数という。
なんだかまた難しい言葉ばかりで、嫌になってきた。
言葉は難しいけれど、実はもう今まで使ってきているよ。
太郎くんは「\(x^2\)」のことはなんて読んでいるかな?
そう、「xの2乗」だよね。
「aをn個掛けた累乗」をan(aのn乗)と書き・・・
これと同じことだよ(笑)
「\(x\)かける\(x\)」というように、\(x\)を2個掛けたものを\(x^2\)と書いているし、
「xの2乗」という言葉ももう使ってきているよね。
指数法則の用語を説明!
累乗・指数とは?
でも、ここで新しく登場する言葉もあるね。
「累乗(るいじょう)」と「指数」だね。
累乗とは?
ザックリいうと
同じものを「累(かさねて)乗(かける)」ということ!
「累」という漢字は、糸の上に田という字が乗っているね。
これはもともとは田が3つ乗っていたんだ。
「糸をかさね合わせて太いより糸にしていく」様子がもとになっているんだよ。
3つの田はそれぞれ「小さなかたまり」を表している。
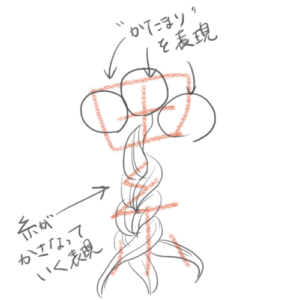
だから、「累」は「かさねる」という意味を持っているんだ。
「乗」は「乗法」という言葉で使っているとおり、「かける」という意味 だよね。
つまり、「累乗」とは「かさねて、かける」ということだよ。
「xの累乗」は、「xをかさねてかけた」ものなんだ。
つまり、「xをくりかえし何個かかけたもの」だね。
ここでハッキリさせておきたいのは、
「同じもの(xならxだけを)をかさねてかける」ということ。
指数とは?
ザックリいうと
「何回」かさねてかけるのかを指示する数のこと!
「指数」の「指」という字も皆はよく使っているよね。
例えば、「指示」なんて言葉で使われているね。
「指示」は「指し示す」という意味。
「こうして」と誰かに命令したり、教えたりするときに使うね。
「\(x\)の累乗」は「\(x\)を何個かかさねてかける」という意味だったね。
でも、「\(x\)の累乗」だけだと、肝心の「\(x\)を何個かけるのか」が分からないよね。
確かに・・
だから、「何個かけるのか?」を伝える「指示」が必要になるんだ。
\(x^2\)は、「\(x\)の累乗で、かける回数は2回だよ!」と
指示しているということなんだ。
指示するための数だから、「指数」なんだ。
ちなみに、この時のxは「底数」と呼ぶんだ。
「底」は「底力」でピンと来ないかな?
「底力」って、「その人のもともと持っていた力のマックス」
という意味だよね。
「底」は「もともと」、つまり「基本」という意味があるんだ。
「\(x\)の累乗」の「\(x\)」は、いわば主役だよね。
\(x\)は基本となるキャラクターなんだよ。
だから「基本となる数」=「底数」と呼ぶ んだ。

なるほどね。
でも、いちいち指数とか累乗とか使わなくても、\(x\)かける\(x\)でいいんじゃない?
なんで勉強が必要なの?
\(x\)かける\(x\)くらいならいいけど、「\(x\)を100回かける」とか言われたら、いちいち全部書くの大変じゃない?

・・・・・・・だね(汗)
「\(x\)を100回かける」を「\(x^100\)」と書くだけで済ませられるなんて、累乗と指数はとても便利だね!
指数法則とは?
言葉にすれば、理解するのはカンタン!
ザックリいうと
指数を持っている数同士を計算するときのルール!
さあ、これで用語の意味は分かったかな?
では、こんどは指数法則とはなにか見ていこう。
「指数」は累乗するときの「指示するための数」だったよね。
この「指数」を持っている数同士を計算するとき、「指数はどうなっちゃうの?」
ということをまとめたのが「指数法則」だよ。
覚える指数法則は、3つだけなんだ。
指数法則、
この3つのルールを覚えよう!
①\(a^m×a^n=\)\(a^{m+n} \)
(累乗の積は、指数の和)
②\((a^m)^n=a^{mn}\)
(累乗の累乗は、指数の積)
③\((ab)^n=a^nb^n\)
(積の累乗は、累乗の積)
またややこしくなってきた!難しそう!
一見難しそうだけど、言っていることは今まで習ってきたことで理解できちゃうよ。
①を例で考えてみるね。
\(a^2×a^3=a^{2+3}\)
つまり、
累乗同士をかけたときは、答えの指数は、かけた累乗それぞれの指数の足し算だよ!
ということを言っているんだ。
「それって本当?」という気もするよね。
試してみよう。
\(a×a\)(\(a\)が2個)\(×a×a×a\)(\(a\)が3個)
\(=a×a×a×a×a\)(\(a\)が5個)
\(=a^5\)
確かに答えの指数「\(5\)」は、かけた累乗それぞれの指数を足した「\(2+3=5\)」と同じだね。
こんなふうに、
もし指数法則を知らなくても、今まで習った知識で計算することもできるよね。
ではなんでこんな法則達を覚えなくてはいけないかというと、
ここから先累乗を含めた整式を掛けたりするときに、
指数法則を知っていればパッパッと計算できて便利だからなんだ。
逆に、知らないとひとつひとつ計算しなきゃいけなかったりで、
とても大変になる。頑張って覚えよう。
②も試してみよう。
\((a^2)^3=a^{2×3}\)
\((a×a)×(a×a)×(a×a)\)
\(=a×a×a×a×a×a\)
\(=a^6\)
確かに、答えの指数「6」は、累乗の指数と、それをさらに累乗するときの指数をかけた「\(2×3\)」と同じだね。
累乗をさらに累乗したときは、答えの指数は
指数同士をかけたものなんだね。
③はどうかな?
\((ab)^2=a^2b^2\)
\((ab)×(ab)\)
\(=a×b×a×b\)
\(=a^2×b^2\)
\(=a^2b^2\)
ある積の累乗は、その指数をそれぞれもつ
累乗の積と同じなんだね。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。






