「展開の公式」例題と解き方解説(パターンは4つ)
高校数学Ⅰ「展開」には、
他にも色々な
工夫のやり方があるよ。
実際のテストでは、これらの
工夫ワザも使う必要があるので、
「どんなワザがあるか」?
を見ていこう。
工夫のワザには大体のパターンが決まっているんだ。
パターン①
積の順番を入れ替える
例題
(x+2)(x+3)(x-2)(x-3)
を展開せよ。
目印は「入れ違いカップル」
 積の順番を入れ替えてあげよう。
積の順番を入れ替えてあげよう。それこそ
「席の順番」を入れ替えるイメージ(笑)
(x+2)(x-2)(x+3)(x-3)
すると、展開の公式
(a+b)(a-b)=a2-b2
が使えるようになる!!
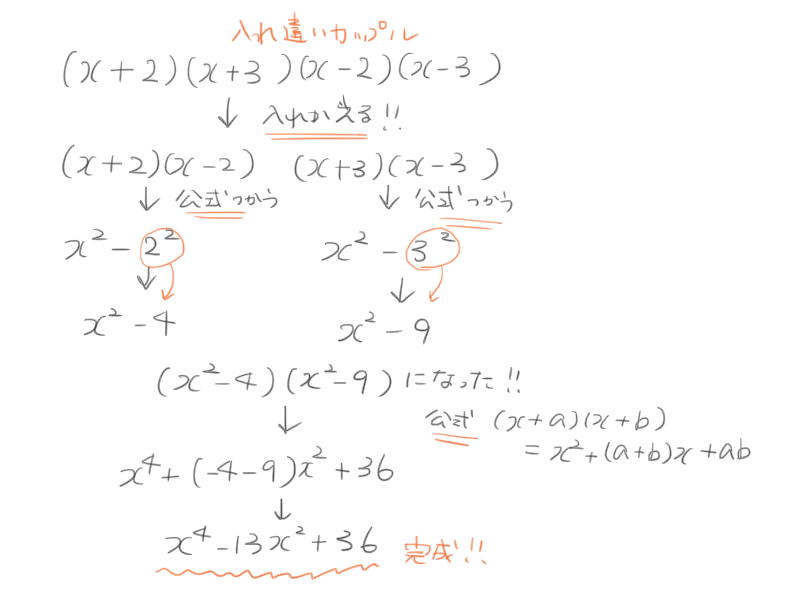
こんなパターンもあるよ。
例題
(x-2)(x+3)(x+1)(x-4)
を展開せよ。
これはカップルは見当たらないけど・・
じゃあカップル予備軍を
探そう。
-2と+1を合わせると -1になるよね。
+3と-4も合わせると -1。
イメージは、
「和が同じ数になる」ように
4つの数字(-2、+3、+1、-4)から
2つのペアを探すんだ。
そして、そのペア同士に積を入れ替える。
(x-2)(x+1)(x+3)(x-4)
=(x2-x-2)(x2-x-12)
どうかな?
(x2-x)
という同じ式が登場したね。
あとはこれをカタマリにするだけ。
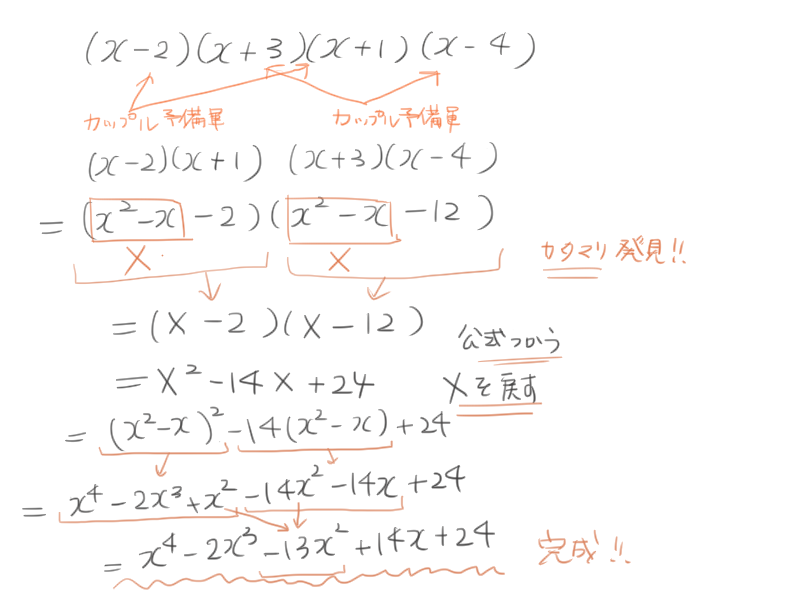
パターン②
符号を揃える
例題
(x-a+b)(x+a-b)
を展開せよ。
カタマリが見つかりそうだけど、
微妙に符号が合わない・・
イメージは
「反対向きにさせたい」から
マイナスと( )で
無理やり振り向かせる!
(x-a+b)(x+a-b)
これを マイナス( )を使えば、
(x-(a-b))(x+a-b)に加工できるんだ!
そうすれば同じカタマリができるね。
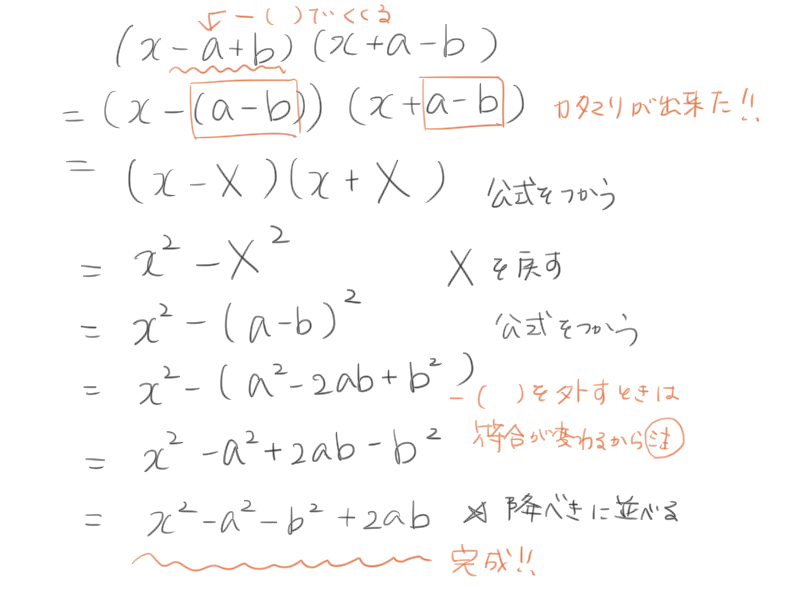
パターン③
指数法則を使う
例題
(x+y)2(x-y)2
を展開せよ。
カタマリもないし、
カップルでもないし・・
これは指数法則を使うよ!
指数法則のひとつに、
(ab)n=anbn
というのがあったよね。
この問題は、
anbn
の形になっているのに
気が付けばカンタン!
(x+y)2(x-y)2
は
(x+y)(x-y)2
に変えられるんだ。
こうやって使うから、
指数法則を学習する必要が
あったんだね。
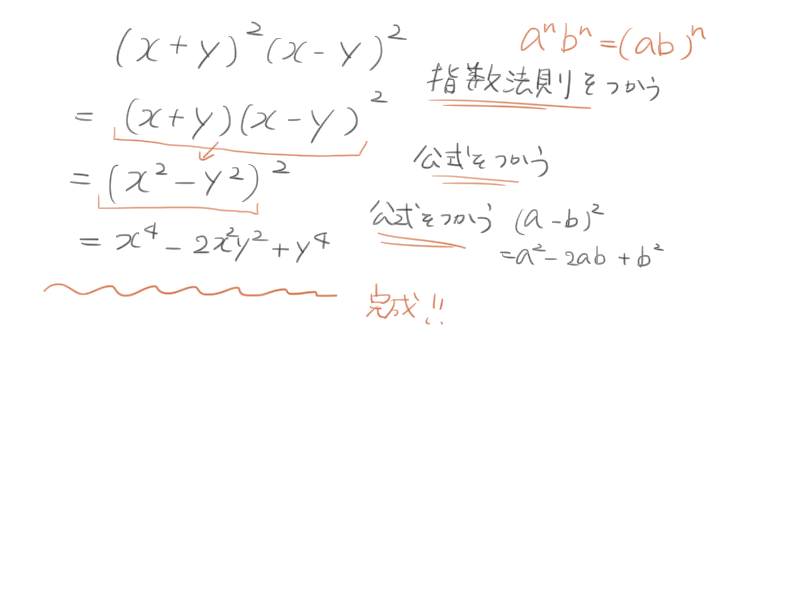
パターン④
公式を使って揃えていく
例題
(a2+1)(a+1)(a-1)
を展開せよ
あれっ
もしかしたら、(a+1)(a-1)を
展開すると、(a2-1)にならない?
その通り!
イメージは親分と子分(笑)
親分の「もと」である子分たちが
合体(展開)して
親分並みの大きさになったイメージ。
実際展開してみよう。
(a+1)(a-1)を展開すると
(a2-1)になるね。
これで
(a2+1)(a2-1)になって、
公式が使えるようになったね。

展開の工夫ワザを使うことで、
計算しなくてはいけない量を
格段に減らすことができるんだ。
それは計算ミスを減らすのに重要だし、計算時間のショートカットができる。
限られた時間で受けるテストには欠かせないワザだね。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。







例が分かりやすくて、理解することが出来ました。
ありがとうございます‼