「整式の加法・減法」をわかりやすく解説(知識編)
「整式の加法・減法」
整式の加法・減法って??
ザックリいうと
「整式同士」を足したり引いたりするだけ!
そもそも、整式の加法・減法って、なにをするの?
そのまんま。「整式」同士を「足したり・引いたり」するだけだよ。
整式の加法・減法は、中学数学の「代入」が分かっていれば実はカンタンなことだから安心してね。
どんな問題が出るの?
まずは、とてもカンタンな問題でどういうことかみてみよう。
問題
次の2つの整式\(A\)と\(B\)について、\(A+B\)、\(A-B\)を計算せよ。
\(A=2x^2+3y\)
\(B=5x^2-y\)
まず、問題は \(A+B\) または \(A-B\) をしなさい
と言っているね。
そして、\(A\)も\(B\)も、それぞれ整式で、
\(A\)は「\(2x^2+3y\)」という整式だよ、と言っていて、
\(B\)は「\(5x^2-y\)」という整式だ、と言っているんだ。
こうやって「整式同士」を足したり引いたりする、というだけ なんだ。簡単だよね。
どうやって計算するの?
ではどうやって計算するかだけど、
「代入」をすればいいだけだよ。
だ、代入・・?
やっぱり難しそう・・
代入というのは、つまり「代わりに入れる」ということだよね。
ここでは、「A」とか「B」という記号の代わりに、「当てはまる整式」を式の中に入れてあげればいいということだよ。
「\(A+B\)」という式の\(A\)と\(B\)に、それぞれの整式を代入するんだ。
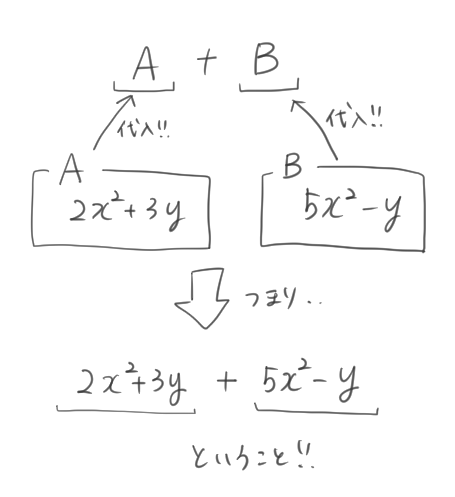
\(A\)は「\(2x^2+3y\)」で、
\(B\)は「\(5x^2-y\)」なんだから、
「\(2x^2+3y\)」+「\(5x^2-y\)」になるね。
あとは、そのまま計算しよう。
\(2x^2+3y+5x^2-y\)
\(=(2+5)x^2+(3-1)y\)
\(=7x^2+2y\)
これで完成。
こうやって横書きで計算してもいいけど、縦に並べて計算する方法もあるよ。
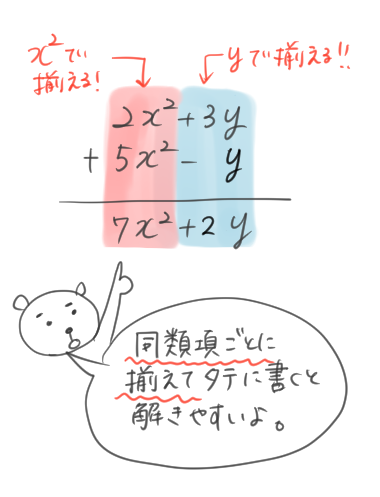
簡単だね。
減法の場合はちょっと注意!!
それでは、「\(A-B\)」の式に代入するとどうなるかな?
「\(2x^2+3y\)」\(-\)「\(5x^2-y\)」になるね。
この時注意なのが、-「 」のカッコを外すときに、符号が変わること。

\(2x^2+3-5x^2+y\)
あとはさっきと同じように、計算するだけだよ。
横書きで計算してみるね。
\(2x^2+3y-5x^2+y\)
\(=(2-5)x^2+(3+1)y\)
\(=-3x^2+4y\)
これで完成!
整式の加法・減法のココを押さえればOK!
まとめ
- 整式の加法とは、「整式同士」を足すだけのこと。
- 整式の減法とは、「整式同士」を引くだけのこと。
- ①問題文にある「A」や「B」の部分に、当てはまる整式を代入する。
- ②加法の場合は、そのまま同類項を揃えて足せばOK!
- ③減法の場合は、まず加法の式に直し、「引く方の整式」のそれぞれの数の符号を変えて、あとはそのまま同類項を揃えて足せばOK!
これが基本の考え方。でも、こんなシンプルな問題ばかりではないのが現実だよね。
テストではこれよりも複雑な形で問題が出てくるんだ。次の記事の「整式の加法・減法(実戦編)」では複雑な問題の出方と解き方を解説するよ。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。






