「整数と小数」とは？整数と少数の仕組みと違いをわかりやすく解説

小学校５年生の算数で学習する「整数と小数」について、整数と小数の仕組み、整数と小数の違いとはなにか、整数と小数を１０倍・１００倍・１０００倍した場合、整数と小数を\(\frac{１}{１０}\)倍、\(\frac{１}{１００}\)倍、\(\frac{１}{１０００}\)倍した場合をわかりやすく解説するよ。

「整数と小数」とは？ 整数と少数の仕組みと違いをわかりやすく解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 整数と小数のしくみ
• １０倍、１００倍、１０００倍してみよう
• \(\frac{１}{１０}\)、\(\frac{１}{１００}\)、\(\frac{１}{１０００}\)してみよう
• まとめ

整数と小数のしくみ

整数せいすうと小数しょうすうがどんな数だったか覚おぼえているかな？
まずは、この２つについて復習ふくしゅうしよう！

ここから２つの数についてくわしく確認かくにんするよ。
２８４９という数は、どんな数が何こあるかを考かんがえてみよう。

２８４９は千の位の数が２、百の位の数が８、十の位の数が４、一の位の数が９ということだから

２８４９＝１０００×２＋１００×８＋１０×４＋１×９

と表あらわすことができるんだ。
※イメージしにくい人は、１０００円札が２枚、１００円玉が８枚、１０円玉が４枚、１円玉が９枚とイメージしてみてね。

つぎに、２.８４９という数も、どんな数が何こあるかを考えてみよう。
２８４９と同じように、それぞれの数字は、その位の数が何こあるかわ表しているから

２.８４９は、一の位の数が２、\(\frac{１}{１０}\)の位の数が８、\(\frac{１}{１００}\)の位の数が４、\(\frac{１}{１０００}\)の位の数が９ということだから

２.８４９＝１×２＋０.１×８＋０.０１×４＋０.００１×９

と表すことができるんだ。

それぞれの位の数字を見てみると
一の位の数が８、\(\frac{１}{１０}\)の位の数が１、\(\frac{１}{１００}\)の位の数が０、\(\frac{１}{１０００}\)の位の数が９ということがわかるね。

だから答えは、
８.１０９＝１×８＋０.１×１＋０.０１×０＋０.００１×９
となるよ。

つぎに、ある数をもとにした数の見方みかたについて考えよう。
「１０円玉が１０枚あったら１００円」になるように、１つの位の数が１０こ集あつまったら、１つ上の位にうつるんだ。
これは小数でも同じことがいえるよ。

すぐに答えを出すのは、難むずかしいからそれぞれの位の数に分けて考えよう。

１.２３４を１＋０.２＋０.０３＋０.００４と考えて、小さい位の数から順番じゅんばんにみてみると
０.００４・・・\(\frac{１}{１０００}\)の位の数が４こ
０.０３・・・\(\frac{１}{１００}\)の位の数が３こ
０.２・・・\(\frac{１}{１０}\)の位の数が２こ
１・・・１の位の数が１こ

と分けることができるね。
これを元にして、それぞれの位の数が０.００１を何こ集めた数かを考えよう。
０.００４
これは、０.００１が４こ集めた数ということがすぐにわかるね！

０.０３
０.００１とくらべてみると、１つ上の位の数ということがわかるね。
０.００１が１０こ集まると、０.０１になるから、０.０３は０.００１が３０こ集まった数ということがわかるよ。

０.２
０.００１とくらべると、２つ上の位の数ということがわかるね。
０.００１が１００こ集まると、０.１になるから、０.２は０.００１が２００こ集まった数ということがわかるよ。

１
０.００１とくらべると、３つ上の位の数ということがわかるね。
０.００１が１０００こ集まると、１になるね。

これで１.２３４は、０.００１を４＋３０＋２００＋１０００＝１２３４こ集めた数、ということがわかるよ。

これまで習ならった数のしくみを使って、つぎの問題にチャレンジしよう。

大きい数も小さい数も、まずは大きい位の数（この問題では十の位の数）から順番に考えることがおすすめだよ。

①つくれる数のうち、いちばん小さい数
いちばん小さい数は、十の位の数から順番に、小さい数を選えらんでいけばOKだよ。
答え　１２.３４５

②つくれる数のうち、２番めに大きい数
まずは、いちばん大きい数から考えよう。
小さい数と同じように、十の位の数から考えればOKだよ。

いちばん大きい数は、５４.３２１になるね。

つぎに、２番めに大きい数について考えよう。
いちばん大きい数の２つの小さい位の数（今回は２と１）を入れ替えると２番めに大きい数を作ることができるよ。
答え　５４.３１２

③つくれる数のうち、５０にいちばん近い数
５０にいちばん近い数も、これまでの問題と同じように十の位の数から考えよう。
５０にいちばん近い数を作る時、十の位の数は「５」か「４」のどちらかになるよ。
※５０にいちばん近い数だと、十の位は「５」だけと考えてしまう人が多いんだけれど、４９.□□□のように、十の位の数が「４」になる時もあるから気をつけよう。

十の位が５で、５０にいちばん近い数
５１.２３４
※５０との差は、１.２３４

十の位が４で、５０にいちばん近い数
４５.３２１
※５０との差は、４.６７９

２つをくらべると、５１.２３４の方が５０に近いことがわかるね。
答え　５１．２３４

１０倍、１００倍、１０００倍してみよう

つぎに、１０倍、１００倍、１０００倍すると、どのような数になるか確認しよう。

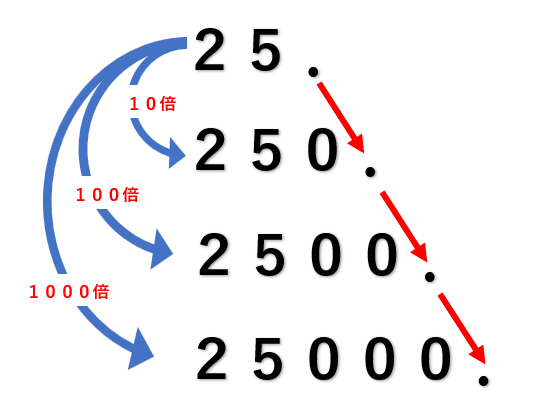
まずは、整数を１０倍、１００倍、１０００倍したものみてみよう。

２５×１０＝２５０
２５×１００＝２５００
２５×１０００＝２５０００

実じつはこれは、２５のうしろに隠かくれている小数点の位置いちが１０倍すると１つ、１００倍すると２つ、１０００倍すると３つ、右にうつっているんだ。

この考え方と同おなじように、小数を１０倍、１００倍、１０００倍してみよう

２.５１×１０＝２５.１
２.５１×１００＝２５１
２.５１×１０００＝２５１０

小数も整数と同じように、小数点の位置が右にうつるんだ。

\(\frac{１}{１０}\)、\(\frac{１}{１００}\)、\(\frac{１}{１０００}\)してみよう

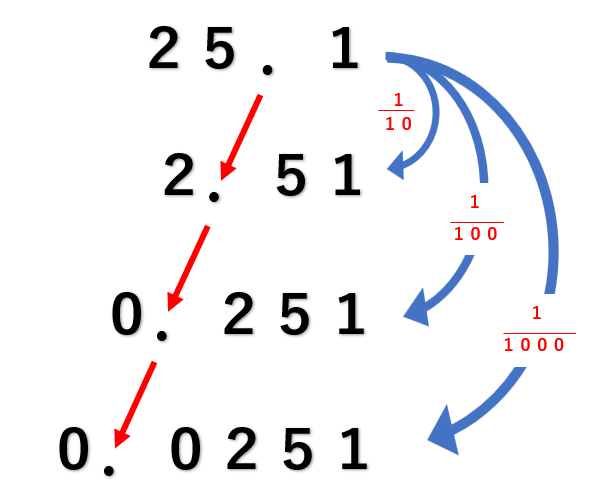
１０倍、１００倍、１０００倍のつぎは、\(\frac{１}{１０}\)、\(\frac{１}{１００}\)、\(\frac{１}{１０００}\)した数について確認しよう。

\(\frac{１}{１０}\)は、１０で割わること
\(\frac{１}{１００}\)は、１００で割ること
\(\frac{１}{１０００}\)は、１０００で割ること
と同じなんだ。

\(\frac{１}{１０}\)した場合　　２５.１÷１０＝２.５１
\(\frac{１}{１００}\)した場合　２５.１÷１００＝０.２５１
\(\frac{１}{１０００}\)した場合　２５.１÷１０００＝０.０２５１

１０倍、１００倍、１０００倍した時と同じように、小数点の位置に注目ちゅうもくすると、\(\frac{１}{１０}\)すると１つ、\(\frac{１}{１００}\)すると２つ、\(\frac{１}{１０００}\)すると３つ、左にうつっていることがわかるね。

整数と小数の仕組みまとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。