「体積の求め方のくふう」複雑な体積の求め方をわかりやすく解説

小学校５年生の算数で学習する「体積の求め方」について、いろいろな形の立体の体積の求め方（複合図形の立体の体積）をわかりやすく解説するよ。

今まで学習した直方体と立方体の体積の求め方をつかって、複雑な体積の求め方を考えてみよう。

「体積の求め方のくふう」複雑な体積の求め方をわかりやすく解説のPDF（5枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

複雑な体積の求め方

直方体や立方体の体積だけではなく、複雑ふくざつな立体の体積を求める問題もテストでは出てくるから、求め方について例題れいだいを使って確認かくにんしよう。

例題
下の図のような形の体積を求めましょう。

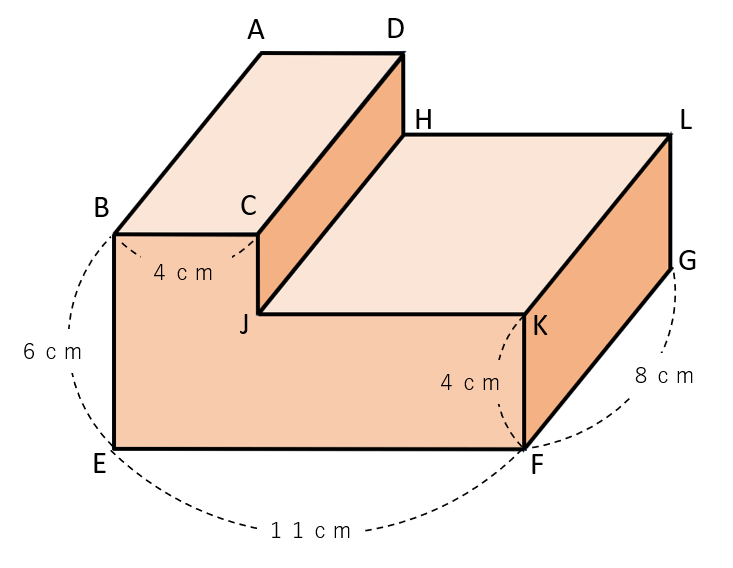
上の例題のような、複雑な立体の体積を求める方法は『いくつかの立体に分けて計算する方法』と『大きな立体から余分よぶんな立体を引いて計算する方法』の２パターンあるよ。

まずは下の図のように、図形を分けて考えてみよう。

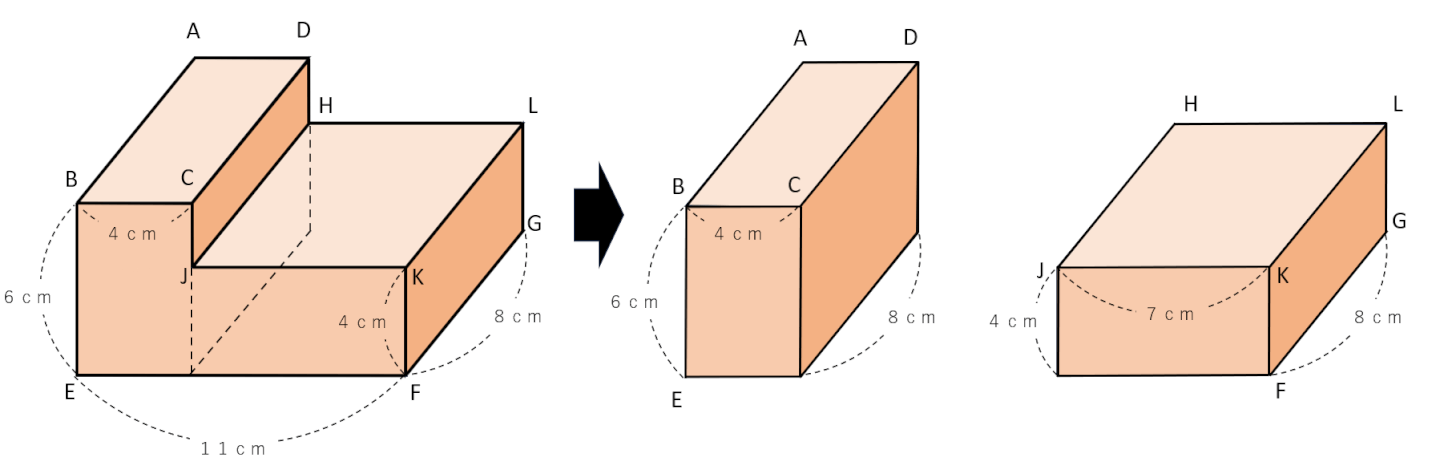
直方体２つに分けることができるから、あとは公式を使って計算をしよう。
（式）８×４×６＋８×７×４＝１９２＋２２４
　　　　　　　　　　　　＝４１６
答え　４１６ｃｍ^３

ちなみに、下の図のように分けることもできるよ。

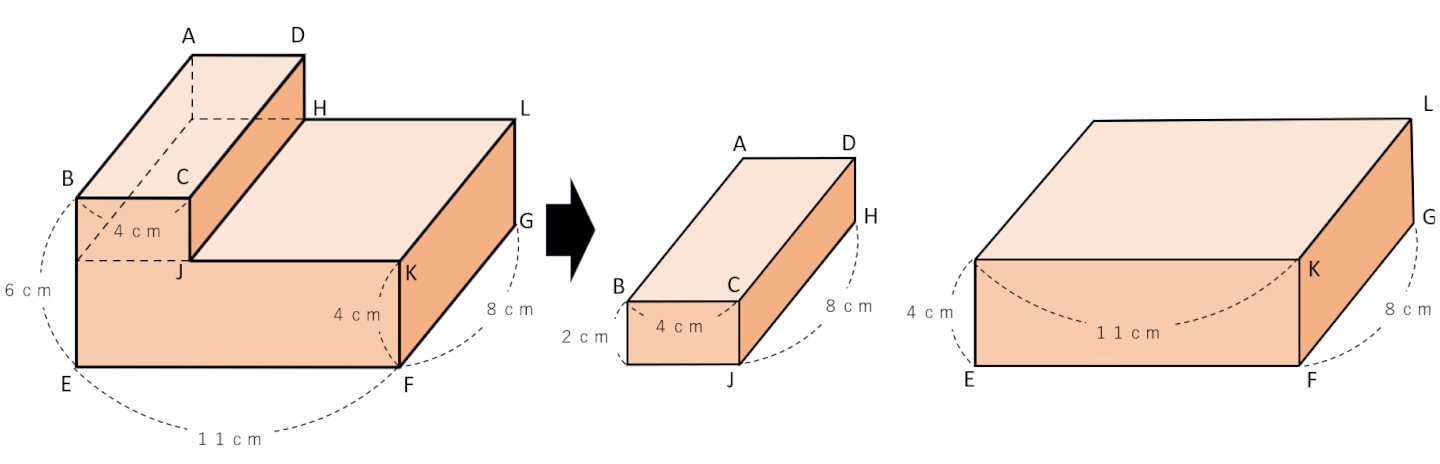
同じように直方体の体積を求める公式を使って計算しよう。
（式）８×４×２＋８×１１×４＝６４＋３５２
　　　　　　　　　　　　　＝４１６
答え　４１６ｃｍ^３

図の分け方は違ちがうけれど、答えは同じになったね。
計算しやすい分け方を自分で見つけられるようにしよう。

下の図のように、元の立体に青い立体を付け加えて、大きな直方体の体積を求めてから余分な立体（付け加えた立体）を引いて計算しよう。

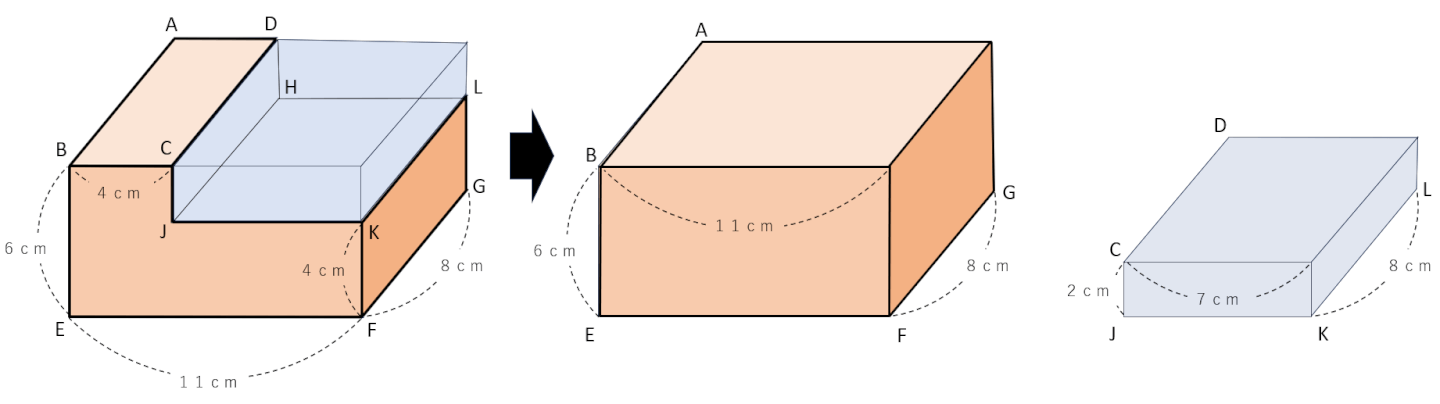
（式）８×１１×６－８×７×２＝５２８－１１２
　　　　　　　　　　　　　＝４１６
答え　４１６ｃｍ^３

上の①で求めた体積と同じ答えになったね。
どちらの方法でも解くことができるように、練習問題にチャレンジしよう。

問題
下の図のような形の体積を求めましょう。

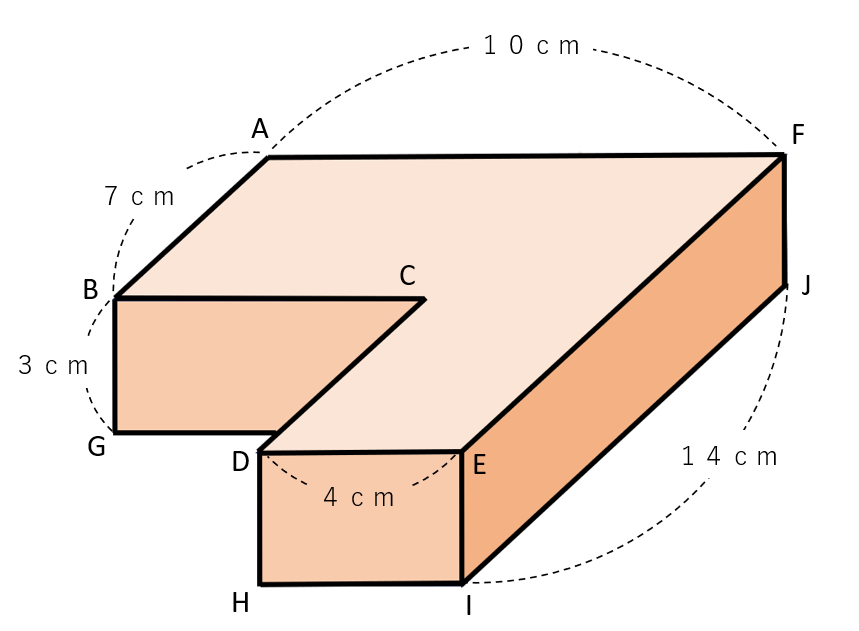
上の例題のように、『いくつかの立体に分けて計算する方法』と『大きな立体から余分よぶんな立体を引いて計算する方法』のそれぞれの方法で求めてみよう。

まずは下の図のように、図形を分けて考えてみよう。

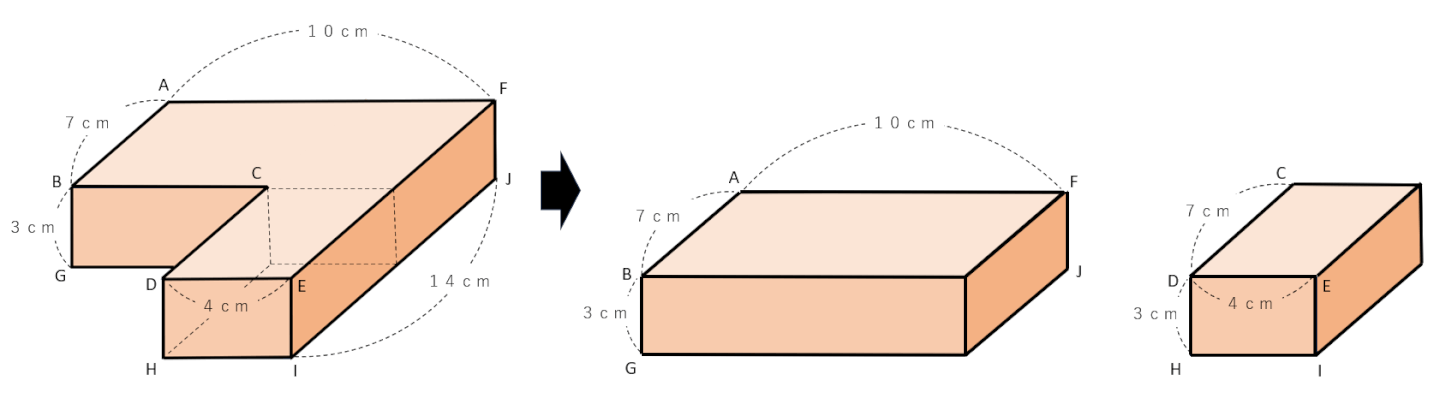
２つに分けた直方体の体積を公式を使って求めよう。
（式）７×１０×３＋７×４×３＝２１０＋８４
　　　　　　　　　　　　　＝２９４
答え　２９４ｃｍ^３
※別な分け方をして求めても同じ答えになるよ。

下の図のように、元の立体に青い立体を付け加えて、大きな直方体の体積を求めてから余分な立体（付け加えた立体）を引いて計算しよう。

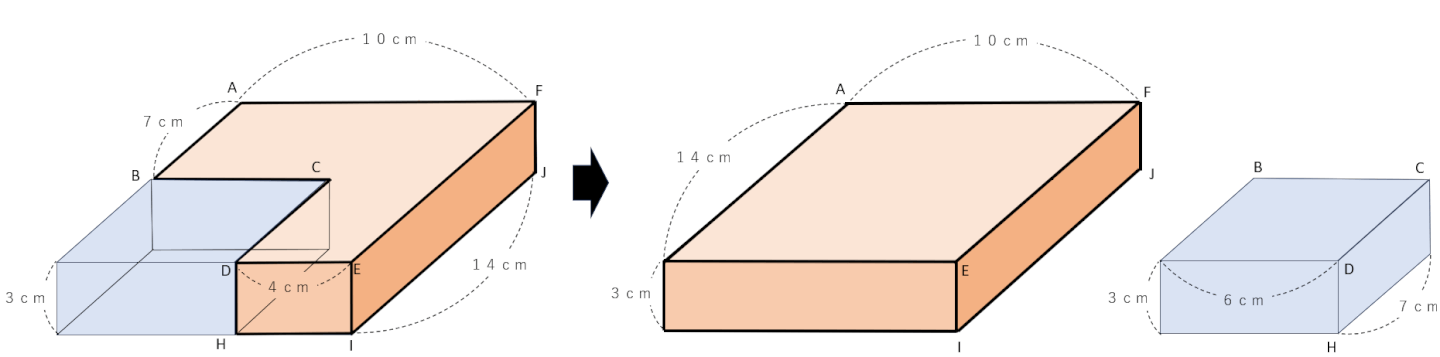
（式）１４×１０×３－７×６×３＝４２０－１２６
　　　　　　　　　　　　　　＝２９４
答え　２９４ｃｍ^３

計算ミスをしているかもしれないと不安な時は、それぞれの解き方で体積を求めて同じ答えになるかを確認しよう。

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。