「体積の求め方」体積とは？体積の単位と公式をわかりやすく解説

小学校５年生の算数で学習する「体積」について、体積とは何か、体積の単位と体積の求め方の公式をわかりやすく解説するよ。

直方体と立方体の体積の公式、体積を求める練習問題の解き方もくわしく紹介するよ。

「体積の求め方」体積とは？ 体積の単位と公式をわかりやすく解説のPDF（10枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 体積とは（体積の単位）
• 体積の単位「立方センチメートル（cm３）」
• 体積の表し方
• 直方体の体積の求め方
• 直方体の体積の公式
• 立方体の体積の求め方と公式
• 直方体と立方体の体積をもとめる練習問題
• 体積の求め方（体積の公式）まとめ

体積とは（体積の単位）

小学校３年生の理科で習ならった『体積たいせき』は、算数でも登場とうじょうするんだ。
体積はどんなものだったか思い出しながら、新しい知識ちしきも確認かくにんしていこう。

体積とは

体積とは、「もののかさ」のこと。
※「もののかさ」とは、ものが「入れ物」だったときに、その入れ物にどのくらいの量の水が入るか？でイメージしよう。

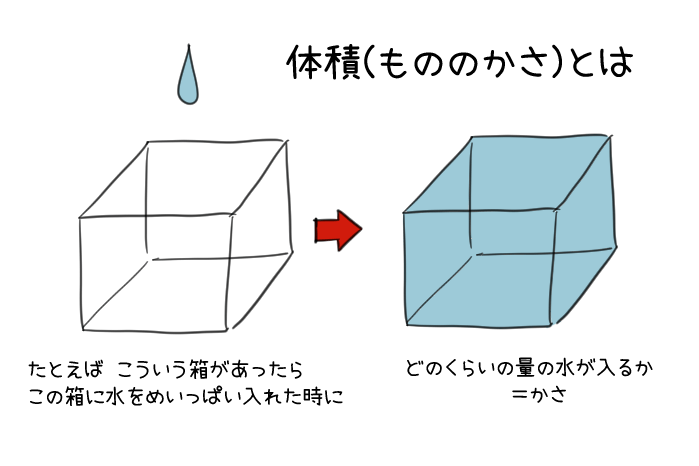
「面積」だったら、これまでにもたくさん学習してきたから、ピンとくるよね。
「面積」はペタンコの「平面」の「広さ」をあらわすものだったよね。
「体積」は、厚さのある「立体」の「かさ」をあらわすものなんだ。

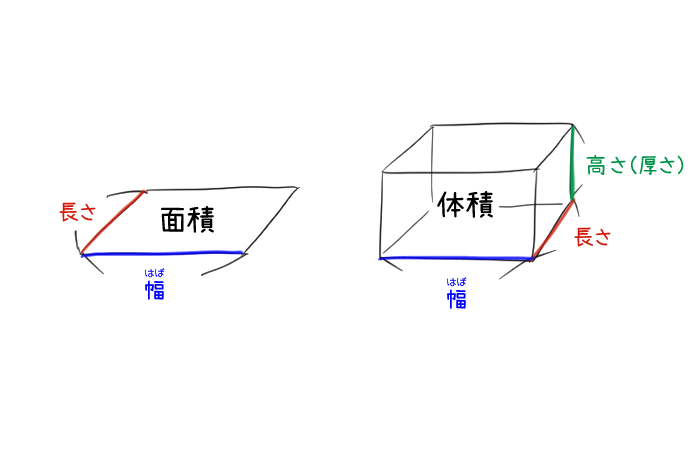
体積の単位「立方センチメートル（cm^３）」

単位（たんい）とは、長さ・重さなど「どのくらいあるか」を計算したり、もとめるときにキホンとなるもののことだよ。

長さだったら、「センチメートル（cm）」とか「メートル（ｍ）」とか、
重さだったら「グラム（ｇ）」とか「キログラム（kg）」とかあるよね。

体積にも、もちろん単位があるよ。

体積の単位は、「立方センチメートル（cm^３）」とか「立方メートル（ｍ^３）」というんだね。

「１ｍＬ」と「１cm^３」の関係

これまでは、「かさ」を表す時には、「水がどのくらい入るか」をイメージするためにも、水の量をあらわす「Ｌ（リットル）」や「ｄＬ（デシリットル）」などの単位を使っていたよね。

これからは、「かさ」を「体積」と呼ぶし、単位も「立方センチメートル（cm^３）」であらわすんだね。

これまでの「かさ」を、「立方センチメートル」で考えるばあい、
１cm^３＝１ｍＬという関係かんけいになるから、忘わすれずに覚おぼえておこう。

体積の表し方

体積の単位「立方センチメートル（cm^３）」について、体積の表し方の考え方をみてみよう。

「立方センチメートル（cm^３）」のばあい、体積は「１辺が１cmの立方体が何こ分あるか」で表あらわしているんだ。

くまごろう

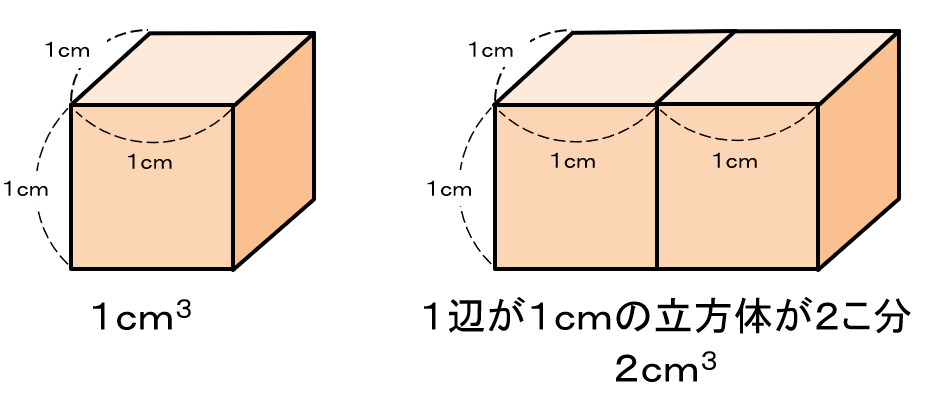
「立方体」とは、６つの正方形で囲まれた立体のことだよ。
「１cm^３の立方体」は、「１辺が１cmの正方形６つでできている立体」ということだね。

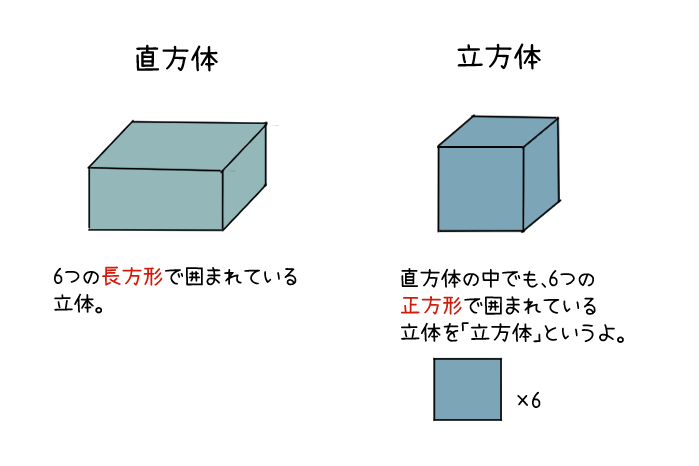
図形の面積をあらわすとき、「１辺が１cmの正方形が何こ分あるか？」という考かんがえ方をするのと同じように、
図形の体積も「もとにする大きさ（たとえば１辺が１cmの立方体）が何こ分あるか？で表す」ということを覚えておこう！

直方体の体積の求め方

それでは、実際に下の直方体の体積を求めてみよう。

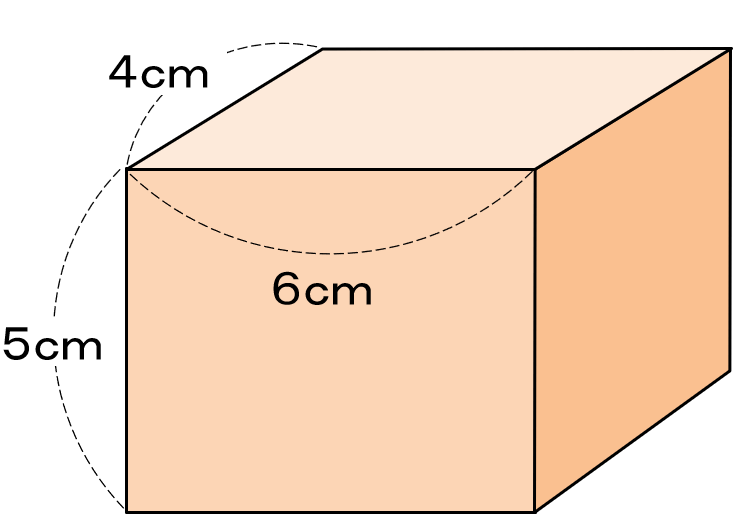
この直方体は、たてが４cm、横が６cm、高さが５cmだね。
この中に「１辺が１cmの立方体」が何こ入れることができるかを考えよう。

まずは、１だんめに何こならべることができるかを考えるよ。

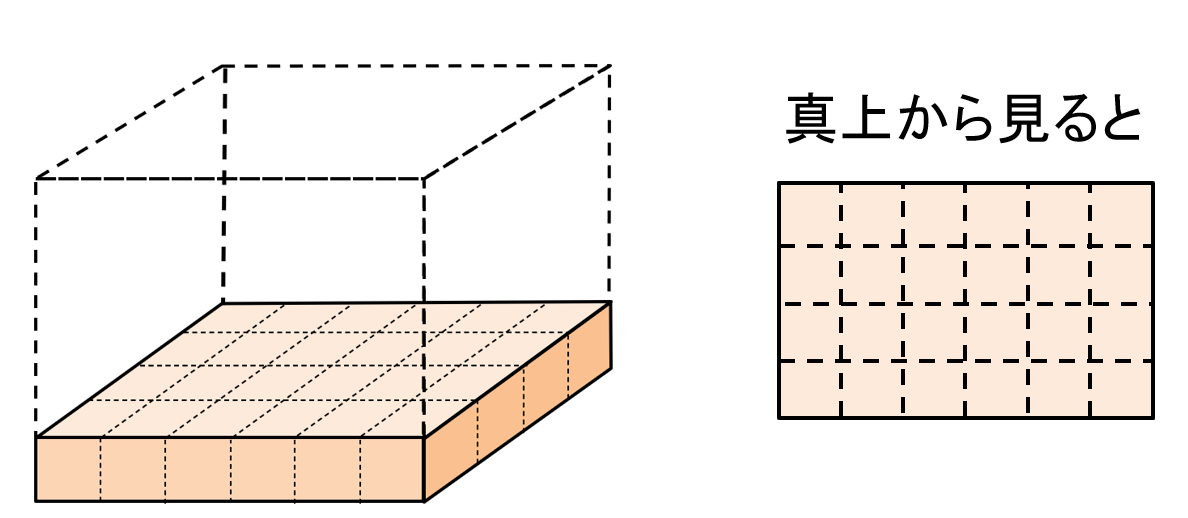
真上から見た図を参考さんこうにするとわかりやすいよ。
たてに４列、横に６列分の立方体をならべることができるね。

だから、１だんめにならべることができる立方体の数は
４×６＝２４（こ）ということがわかるよ。

つぎに「１だんに立方体が２４こあるかたまり」を何だん積めるかを考えよう。

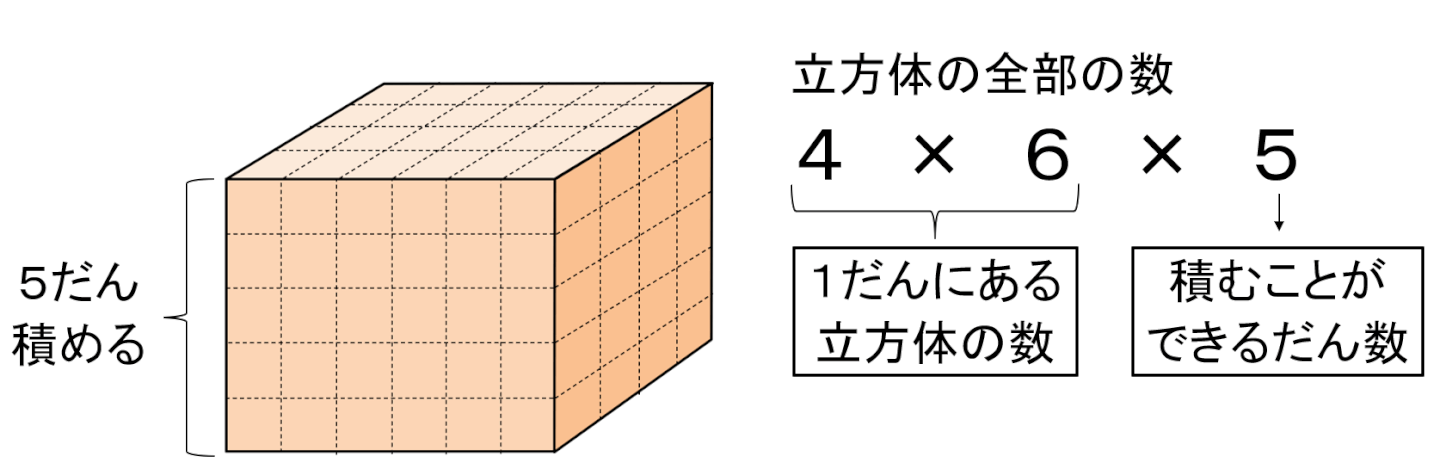
上の図を見てわかるとおり、高さが５cmだから、全部で５だん積めるね。

そうすると、この直方体に１cm^３の立方体を
４×６×５＝１２０（こ）入れることができるから、体積は１２０cm^３と求めることができるんだ。

「１だんに立方体がいくつあるか」をかんがえて、「そのだんが何だん積めるか」を考えると、直方体の体積がもとめられるんだね。

いつもこの解き方をしてもいいんだけれど、たくさん問題が出てきたら大変だよね。
実は体積をかんたんに求めることができる公式があるんだ。

直方体の体積の公式

たてが４cm、横が６cm、高さが５cmの直方体の体積を求める計算は、
４×６×５＝１２０だったね。

体積を求める計算をした時の式と、直方体の「たて・横・高さ」の長さを見くらべてみよう。

計算式「４×６×５」は、直方体の「たて×横×高さ」になっていることに気づいたかな？
実はこの「たて×横×高さ」が直方体の体積を求めるための公式なんだ。

立方体の体積の求め方と公式

つぎは下の立方体の体積を求めてみよう。

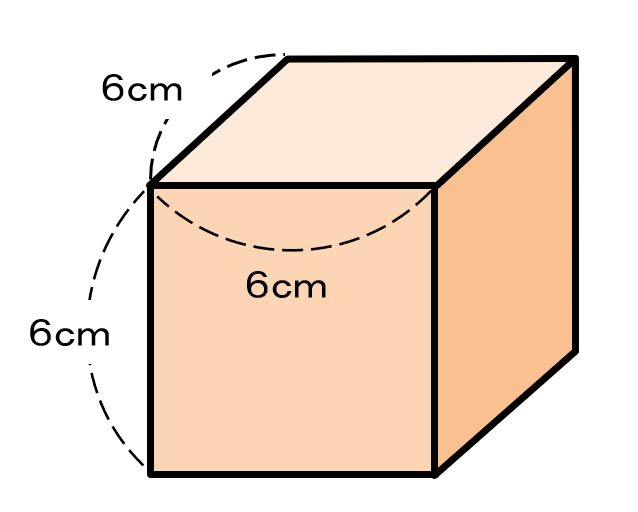
正方形が長方形のなかまであるように、立方体も直方体のなかまなんだ。
つまり、直方体を求める公式を使って、立方体の体積を求めることができるよ。

図からわかるように、たて＝６cm、横＝６cm、高さ＝６cmだから、これを『たて×横×高さ』の公式に代入すると
６×６×６＝２１６（ｃｍ^３）と求めることができるんだ。

ちなみに、立方体は、たて、横、高さがすべて同じ長さだから、どこか1か所の長さがわかれば、体積を求めることができるよ。

直方体と立方体の体積をもとめる練習問題

直方体と立方体の体積を求める公式を使って、練習問題にチャレンジしよう。

問題

下の①から③の直方体や立方体の体積は何cm^３ですか。

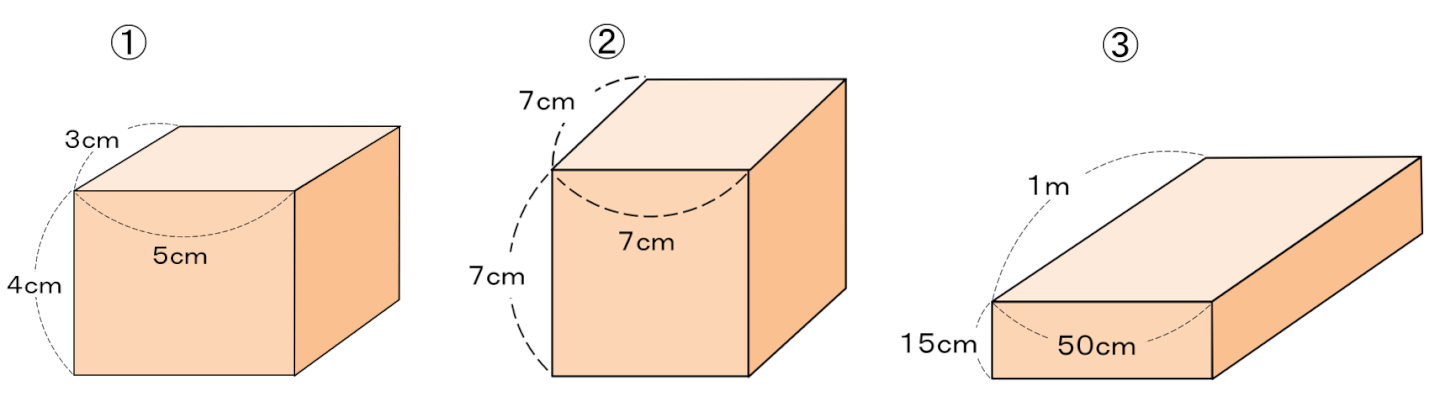
それぞれの「たて・横・高さ」を確認して、公式に代入して計算すればOKだね！

①
たて＝３cm、横＝５cm、高さ＝４cmだから
３×５×４＝６０
答え　６０cm^３

②
この図形は、立方体だね！
１辺の長さは、７cmだから
７×７×７＝３４３
答え　３４３cm^３

③
たての長さが、１ｍとなっているところに注意！
問題では「何ｃｍ^３か」とあるから、単位をcmに直すことを忘れずに！

たて＝１００cm、横＝５０cm、高さ＝１５cmだから
１００×５０×１５＝７５０００
答え　７５０００cm^３

問題

下の図は直方体の展開図てんかいずです。この直方体の体積を求めましょう。

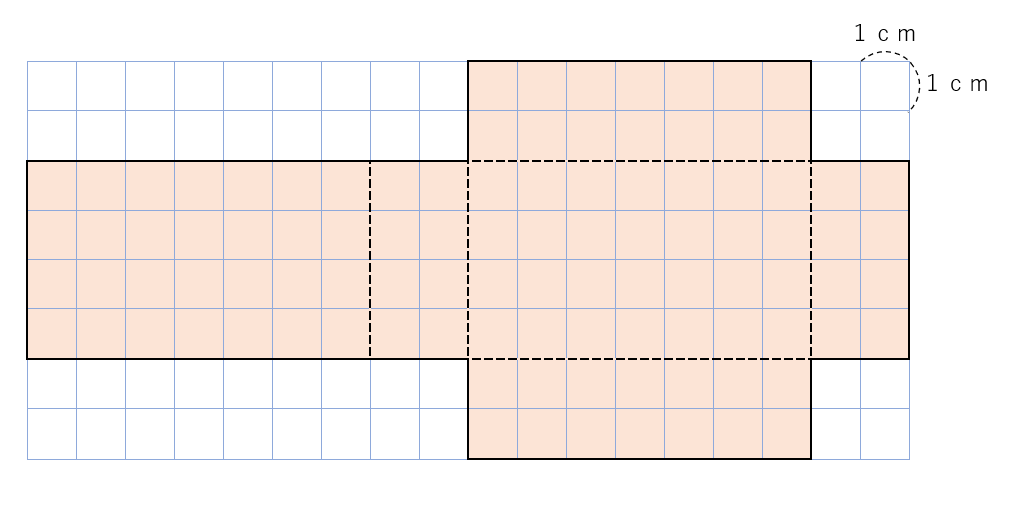
展開図のまま考えるのは難むずかしいから、展開図を組み立てた直方体を描かいて考えよう。

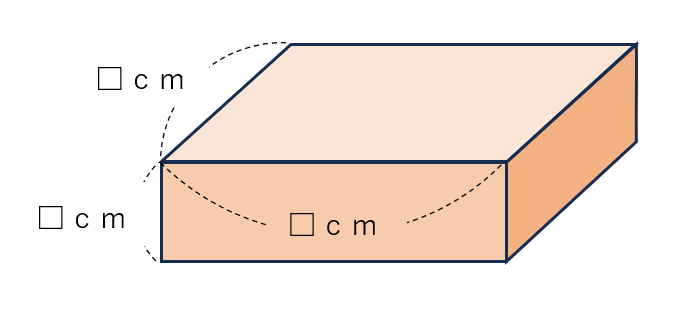
展開図と上の直方体を見比べながら、「たて・横・高さ」を確認しよう。
たて＝４cm、横＝７cm、高さ＝２cmということがわかるから、この直方体の体積は、４×７×２＝５６（cm^３）と求めることができるよ。
答え　５６cm^３

体積の求め方（体積の公式）まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

1. 匿名 より:

   2024年4月1日 7:45 PM

   体積の求め方が分かった。説明が分かりやすかった。

   返信