割合の問題の解き方(応用問題)
割合の問題はどんなふうに出るのか?割合の応用問題の解き方をひとつずつくわしく解説。
割合とはそもそも何か、どうやって求めるのかピンとこなかったら、割合についての解説ページを先に確認しよう!
目次【本記事の内容】
割合の応用問題
「比べられる量」を求める
割合の基本問題では、「比べられる量」と「もとにする量」が分かっていて、そこから割合を求めたよね。
応用問題のパターンの1つは、この「分かっているもの」がメンバーチェンジするというもの。
このパターンの問題を解くポイントは、
「式の関係をもとに、かくれているところはどこかを意識する」ことだよ。
今はピンとこなくても、くわしく説明するから安心してね。
実際に、問題を解きながら考えてみよう。
問題例
太郎くんのクラスには40人の生徒がいます。クラスメイト全員にペットを飼っているかアンケートをとったところ、25%の生徒がペットを飼っていました。
ペットを飼っている生徒の人数を求めましょう。
まず、基本問題を解いていたときに使っていた式を思い出そう。
割合=比べられる量÷もとにする量
だったね。
さて、この「割合」「比べられる量」「もとにする量」って、それぞれどういう関係なんだろう?
「みはじ」の公式を思い出してみよう
ちょっとここで、「みはじ」の公式のことを思い出してみて。
「速さ」「時間」「道のり」の公式だね。
速さ=道のり÷時間
というように、「速さ」は「道のり」を「時間」で割って求める、という式のことだね。
このとき、「速さ」と「時間」「道のり」それぞれの関係は下のような図であらわすことができるよね。
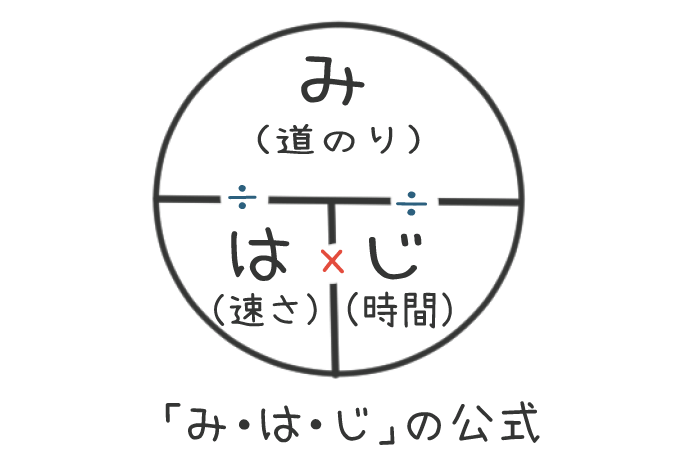
この図を使えば、例えば「時間」が分からないときでも、「道のり」÷「速さ」で求めることができる、とか
「道のり」が分からなくても、「速さ」と「時間」をかければ求めることができる、なんてことが分かるよね。
割合の式もおんなじだよ。
「割合」「比べられる量」「もとにする量」の関係を図にすると下のようになるんだ。
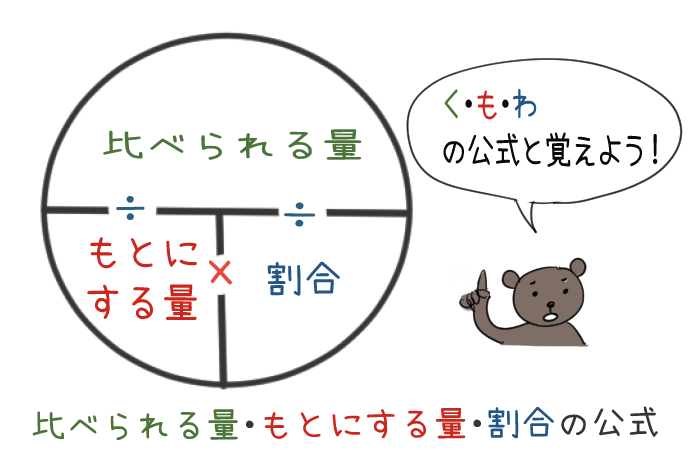
つまり、この図をつかえば「比べられる量」が分からなかったり、「もとにする量」が分からないときでも、残りの2つが分かっていれば計算できるということだね。
では、もう一度問題文を確認してみよう。
問題例
太郎くんのクラスには40人の生徒がいます。クラスメイト全員にペットを飼っているかアンケートをとったところ、25%の生徒がペットを飼っていました。
ペットを飼っている生徒の人数を求めましょう。
この問題文の中から、「割合」と「比べられる量」、「もとにする量」それぞれを探し出そう。
「40人の生徒がいます」…これは、「もともとクラスに何人の生徒がいるか」ということを言っているんだよね。
つまり、これが「もとにする量」だね。
「25%の生徒」…%を使っているということは、これが「割合」だね。
「ペットを飼っている生徒の人数」…もともとのクラスの人数に比べて、「ペットを飼っている生徒はどのくらいいるのか?」と言っているんだよね。
つまり、これが「比べられる量」だね。
さて、3つのうち、どれが分かっていないのかな?
「もとにする量」は「40人」だね。
「割合」は「25%」だね。
「比べられる量」は…何人かは分からないね。
そうだね。この問題は、「比べられる量」が分からない問題だね。
でも残りの2つ「もとにする量」と「割合」が分かっているから、さっきの図を使えば計算ができるね。
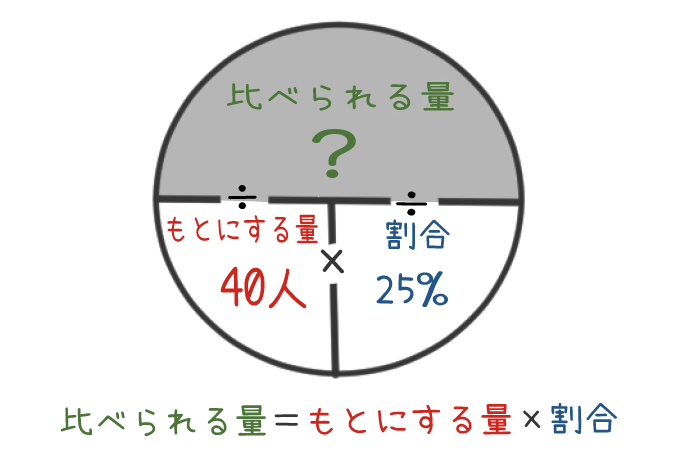
そうか。
比べられる量は、「もとにする量」に「割合」をかけてあげればいいんだね。
これをさっきの問題で計算してみよう。
ペットを飼っている生徒の人数 = 40人 × 25%
ここでひとつ注意。
25%は、百分率で表しているものなので、そのままでは計算ができないよ。
「小数で表す割合」に直してあげよう。
ペットを飼っている生徒の人数 = 40 × 0.25
=10
答え:10人
百分率を小数で表す割合に直す方法がわからなかったら、「歩合・割合・百分率」の関係について解説しているページをチェックしてね。
「比べられる量」を求める割合の問題の解き方
① 「もとにする量」と「割合」を問題文から探そう
② 割合が百分率や歩合の場合は、小数に直そう
③ 「もとにする量」に「割合」をかけよう
割合の応用問題
「もとにする量」を求める
問題例
太郎くんの来月からのお小遣いは1500円で、これは今までのお小遣いの120%です。
今まではいくらのお小遣いをもらっていましたか。
この問題では何が分かって、何が分からないのかな?
「来月からのお小遣い1500円」…これは今までのお小遣いと比べて120%の金額だね。
つまり、「比べられる量」だよ。
「120%」…これが「割合」だね。
「今まではいくらのお小遣い」…もともとのお小遣いの金額、という意味だよね。
つまり、これが「もとにする量」だね。
「比べられる量」は「1500円」
「割合」は「120%」
「もとにする量」は…これが分からないね。
分かっているものと、分からないものが決まれば、あとはさっきと同じように図に当てはめて考えてみよう。
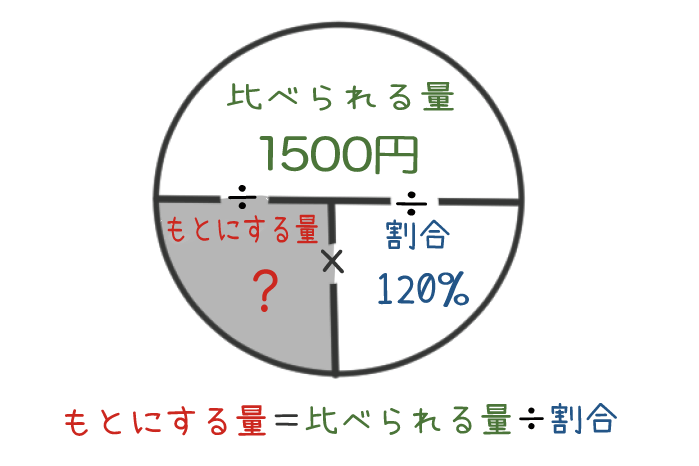
120%は、さっきと同じように小数の1.2に直して計算するよ。
今までのお小遣い=1500 ÷ 1.2
=1250
答え:1250円
「もとにする量」を求める割合の問題の解き方
① 「割合」と「比べられる量」を問題文から探そう
② 割合が百分率や歩合の場合は、小数に直そう
③ 「くらべられる量」を「割合」で割ろう
割合の応用問題まとめ
- 「割合」「比べられる量」「もとにする量」を問題文から探そう
- 「分かっているもの」と「分からないもの」を確認しよう
- 「比べられる量」が分からない場合は、
「もとにする量」×「割合」で求めることができる - 「もとにする量」が分からない場合は、
「比べられる量」÷「割合」で求めることができる - 「割合」が百分率や歩合で表されているときは、小数に直してから計算しよう
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

-
-
比べる量=もとにする量×割合
ですよ。
式が逆になってます。 -
比べる量=もとにする量×割合
ですよ。
式が逆になってます。 -
この「みはじ」とかいうてんとう虫みたいな公式(公式とは呼びたくない)を教えるせいで子どもの数学力が伸びないと個人的には思っております。
-
おこづかいの解答まちがってませんか?






比べる量=もとにする量×割合
ですよ。
式が逆になってます。