「部分集合・共通部分・和集合」記号の覚え方と意味を解説
部分集合・共通部分・和集合とは?記号はどうやって覚えたらいい?
高校数学Aで学ぶ「部分集合・共通部分・和集合」について、言葉の意味や記号の意味をイラストや身近なたとえを使ってわかりやすく解説します。
「集合」って何?と思ったら、「集合と要素」の解説ページからチェックしよう。
「部分集合・共通部分・和集合」
目次【本記事の内容】
- 1.部分集合・共通部分・和集合とは
- 2.部分集合とは
- 3.共通部分とは
- 4.和集合とは
- 5.空集合とは
部分集合・共通部分・和集合とは
教科書の説明
集合A、Bのどちらにも属する要素全体の集合をAとBの共通部分といい、A∩Bで表す。
集合A、Bの少なくとも一方に属する要素全体の集合をAとBの和集合といい、A∪Bで表す。
要素をもたない集合を空集合といい、記号øで表す。
またわけのわからない言葉ばかり出てきた!記号もまるで間違い探しレベルだよ(泣)
たしかに。
ここの記号は上下左右の向きがどれだったか思い出せなくて困る人が多いよ。
ザックリいうと?
ザックリいうと
グループ同士の関係を表す言葉!
「集合A」とか「集合B」とか呼ばれている「集合」というのは、つまりは
「グループみたいなもの」だったよね。
この集合Aとか集合Bとか呼ばれているグループ同士が、どんな関係なのか?によって、「部分集合とか共通部分、和集合」なんていう色んな呼び方をしているだけ なんだ。
グループ同士の関係を表す「ベン図」
この「グループ同士がどんな関係なのか?」を表すのに便利なのが、「ベン図」。
ベン図・・・・?
不思議な名前だね。
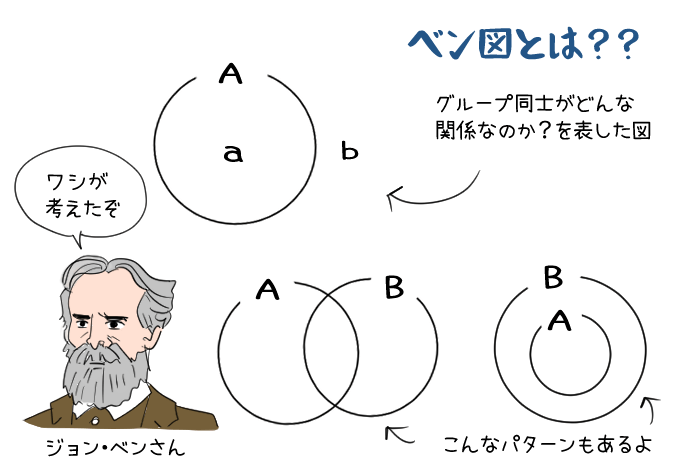
「この図を描いたら関係性がわかりやすいじゃん!」と、発見した人の名前がベンさんだから「ベン図」と言うんだよ(笑)
それでは、それぞれ例をあげながら解説していくよ。
部分集合とは
集合Aのすべての要素が集合Bの要素になっているとき、AをBの部分集合といい・・
通訳するよ。
「Aグループのメンバーが全員Bグループでもある」なら、AグループはBグループの「部分集合」と呼ぶよー。 と言ってるんだ。
学校のクラスで例えてみよう。
たとえば、
- Bグループというのは「1年1組」のこと。
- Aグループというのは「1年1組の2班」のこと
Aグループの「1年1組の2班の生徒たち」って、同時に全員がBグループの「1年1組の生徒」でもあるよね。
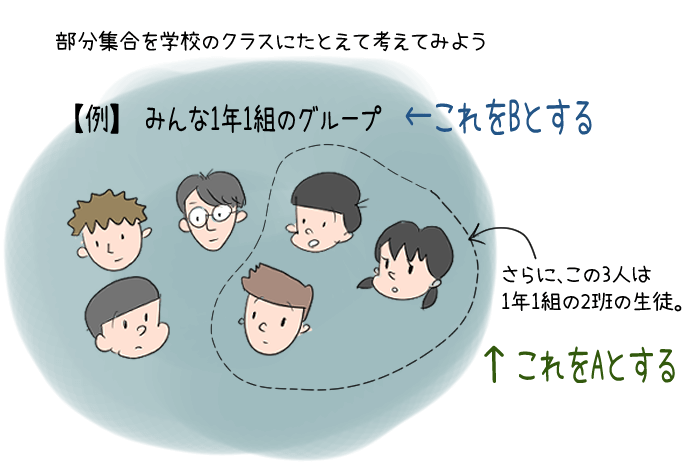
Aグループのメンバー全員が、Bグループのメンバーでもあるという関係だね。
そんな関係を、「部分集合」と呼ぶよ、ということなんだ。
ベン図にすると、こんな感じだね。
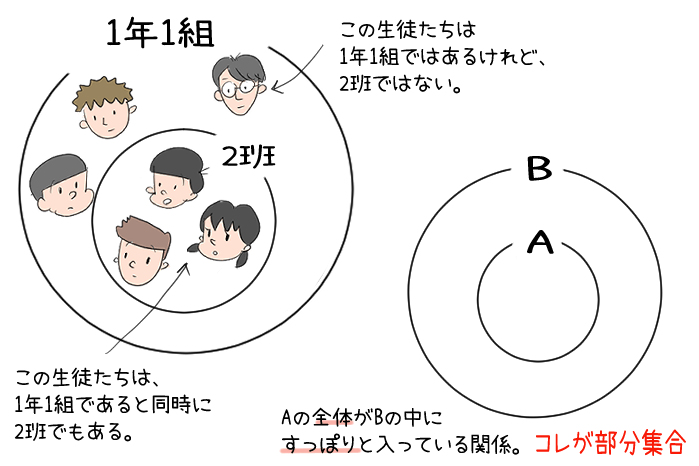
続けるよ。
・・A⊂BまたはB⊃Aで表す。
これは、この関係を記号で表す方法もあって、A⊂B、またはB⊃Aと書くよ、と言っているだけだね。
なるほど。
言っていることは分かったけど、記号の向きが覚えづらいな・・
部分集合の記号の覚え方
部分集合のカッコが、どっち向きで書けばいいか迷ってしまうことがあるよね。
部分集合の関係は、
親グループが、子グループをぐるっと囲って捕まえているようなイメージだよね。
そう考えると、部分集合の記号のカッコの向きは、親グループが子グループを捕まえようと追いかけているみたいだね。
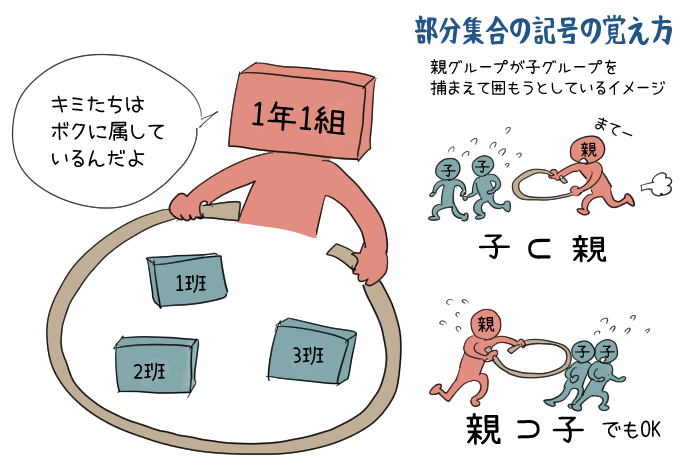
このとき、輪っかが開いている側が親グループだね。輪っかの開いてる側が親グループ側になっていれば並び順や⊂の向き(右向き・左向き)はどちらでもいいんだ。
共通部分とは
集合A、Bのどちらにも属する要素全体の集合をAとBの共通部分といい、A∩Bで表す。
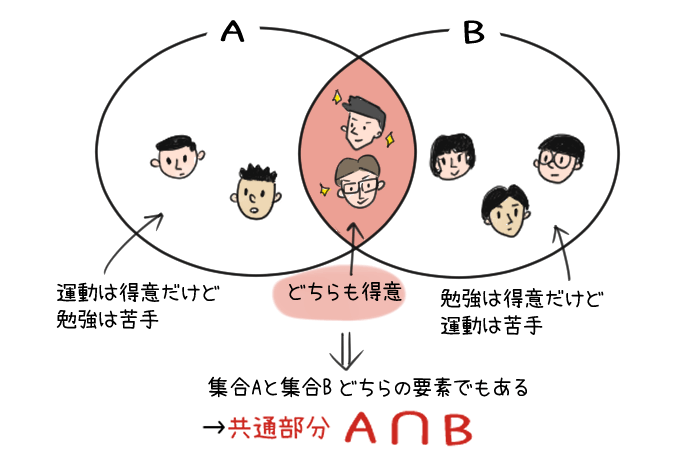
コレは「グループAでもあるし、グループBでもあるという人たちの集団のことを共通部分って呼ぶよー」という意味だよ。
学校のクラスで考えてみよう。
クラスの生徒の中で、
「運動神経がいい子(体育が5)」を「Aグループ」として、
「頭がいい子(テスト平均が90点以上)」を「Bグループ」としてみよう。
こんなとき、「体育の成績は5で、さらにテストの平均も90点以上を取っちゃう」文武両道タイプの子っているよね。
つまり、「運動神経もいいし、なおかつ頭もいい」俗に言う「出来杉君」的な子たちだね。
これって、「運動神経がいいAグループ」と、「頭がいいBグループ」が重なっているイメージなんだ。
この「重なっている部分」を「共通部分」と呼ぶ、ということ だよ。
簡単だね。
記号で表すときは、「A∩B」と書けばいいんだ。
(読み方は「AかつB」だよ)
共通部分の記号の覚え方
記号「∩」のイメージは、限られたメンバーだけでくるまっているイメージかな。

部分集合との違いは、「ひとつのグループが、もうひとつのグループにすっぽり入っているかどうか」だね。
和集合とは
では
和集合:集合A、Bの少なくとも一方に属する要素全体の集合
これは「運動神経がいいか、頭がいいか、の少なくてもどっちかの子達」ということを言ってるんだ。
記号では、「A∪B」と書くよ。
(読み方は「AまたはB」)
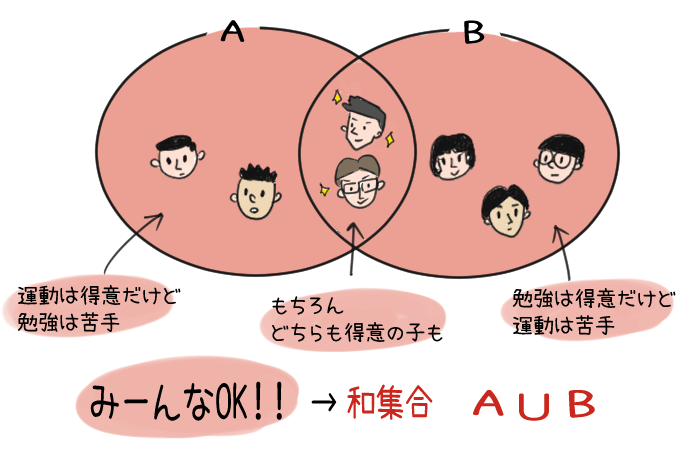
このとき注意が必要なのは、「少なくてもどちらか」なので、運動神経もよくてなおかつ頭がいい子ももちろん入るよ。大いに越したことはないということなんだ。
だって、もし君が友達に、「頭がいい」または「運動神経抜群」の男の子を紹介して!と言われたら、「「頭が良くてなおかつ運動神経抜群」の男の子はダメか・・」なんて考えないよね(笑)
記号「∪」は皆ひっくるめて、ぐるっと囲っているイメージだね。

空集合とは
最後に、
空集合:要素をもたない集合
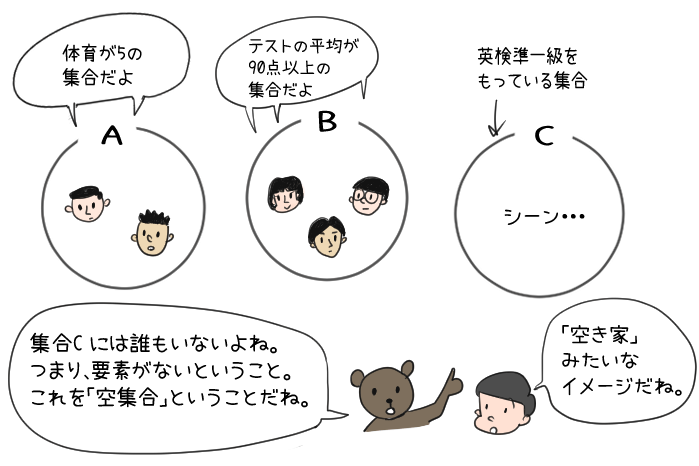
簡単に言えば「メンバーがいない」「該当者がいない」グループのことだよ。空っぽだから、空集合なんだね。
例えば1年1組の生徒には「英検準1級を持っている生徒」がゼロならば、
「英検準1級を持っている」グループは空集合だね。
空集合は ø と書くよ。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。

-
-
とてもわかりやすかったです!ですが、すぐに忘れてしまあかそうです、。










ゆみねこ様、はじめまして。ソリテュードと申します。(ソロでも構いません)
この度、ゆみねこ様の記事(主に高校数学)を拝読しました。
身近なもので例えたり、時々クスッと笑えるイラストのお陰で、とてもわかりやすいです。
お恥ずかしながら、私は現在、働きながら学び直しを行っている身で、「中学数学・高校数学」をメインに
勉強しています。
私事ですが…学習障害(算数障害の類)を持ってる身故、参考書等で記載されてる内容を、上手にイメージすることが難しいのです…
ゆみねこ様は、身近な物事、日常生活で例えた内容は(集合の要素の⊂など)、私にとっては大きな救いとなっております。
心より、感謝申し上げます。
P.S 長文失礼致しました
ソリテュード