項・次数・係数とはなにか数学用語をわかりやすく解説
「式の整理」とは? 何のために勉強するの?
数学Ⅰの最初に学ぶのは、「式の整理」についてだよ。
式の整理とは、そのまま、「複雑な式をカンタンにしたり、綺麗にしたり」すること。
なぜ、そんなことをする必要があるのか?というと、
これから先は、中学校で習った「展開」とか「因数分解」の「ハイレベル」な
問題が出てきたりするんだけど、その時に出来るだけ「式をカンタンにする」ワザが
必要になるからなんだ。
学校の教科書だと、いきなり「式を整理しよう!やり方はこうだよ!」と、訳も分からずにスタートさせられてしまうよね。
人間、「なぜそれをする必要があるのか?」が分からないことにはあまり興味を持てないと思うんだ。
ただの「作業」になってしまって、必要なくなったら「忘れてしまう」のではないかな?
このサイトでは、「そもそもなぜこの知識は必要なのか?」「何が目的か」を意識しながら説明できたら良いなと思っているよ。
話は戻って・・
例えば、お料理で考えてみよう。
中学校までは、簡単に「塩こしょう」して「焼く」だけで済む「鳥の塩焼き」なんて
料理を作っていたとするよ。
高校からは、「鳥から揚げのオイスターソース和え」なんて、ややこしい料理が
登場する。
調味料も「酒・みりん・醤油・オイスターソース・・・」など複雑だし、
調理方法も「まぶす・揚げる・炒める・和える」なんて色々だ。
そこで、調味料をひとつずつ計って加えるのは大変だから、
事前に「混ぜ合わせておこう」
とか、
調理で使う道具は、使う順番に「並べておこう」
なんて工夫が必要になる。
つまり、「式の整理」を学ぶ目的は、「高校数学で習う複雑な計算にアタフタしないように、工夫のワザを覚える」
ということだよ。
必要になる用語の解説
まず、そのワザを覚える前に、重要な用語を確認しよう。
※料理でも、オイスターソースがなにか、片栗粉はなにか、知らないと出来ないよね?
・単項式/多項式
・次数/多項式の次数
・係数
・○○についての整式
・定数項
それぞれ説明していくね。
もうわかっている用語は飛ばしてもいいよ。
単項式/多項式とは・・・
そもそも「項」ってなんだったか覚えているかな?
ある数式(数を使った式)があったとき、
その数式を説明するのに「+(足す)しか使っちゃダメ!」縛りされていたとしよう。
つまり、「-(引く)、×(かける)、÷(割る)」は使えないよ。
これを、教科書では
加法だけの式に直す
なんて難しい言い方をしているよ。
たとえば、
\(1+8-5\)
なんて数式があったとする。
\(1+8\)までは「+しか使っていない」からいいよね。
でも、\(-5\)は「引く5」と言ってはいけないので困ってしまうよね。
では、どうすればいいかな?
ちょっとヒネクレた言い方なんだけど、
「-5」を「足す」って言えばいいんだ。
\(-5\)を足すと、結局は5を引くことになるからね。
ということは、さっきの数式を全部同じ考え方で言い換えると・・
「\(+1\)」足す「\(+8\)」足す「\(-5\)」となる。
つまり、「\(+1\)」+「\(+8\)」+「\(-5\)」これが、
「加法だけの式に直した」状態なんだ。
こうやって
「加法だけの式に直した」とき、+と+の間の「」で区切られたものが「項」だよ。
身近イメージで伝えるために、カードゲームに例えてみるよ。
「カードを順番に何枚か引いていって、書いてある数字の合計が自分のポイントになって、より多いポイントをゲットした人が勝ち」
というゲームがあったとするよね。
そのカードには、「+1」カードもあれば、「-5」なんてカードもあるんだ。
「-5」は「引いてしまうとガッカリなカード」と言ったところかな。
引いたカードが「+1」「+8」「-5」だったら、
その場合の獲得ポイントは
\(1+8-5=4\)ポイントだよね。
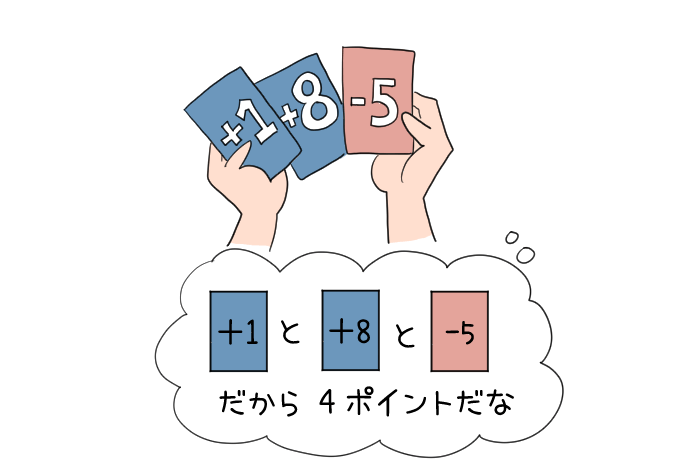
このときの-5は、あくまで「-5」というカードを「ゲットした(加えた)」 「項」は、この「カード1枚1枚」のイメージだよ。
として計算していて、「せっかく持っていた「5」というカードを手放した(引いた)」
という事ではないよね。
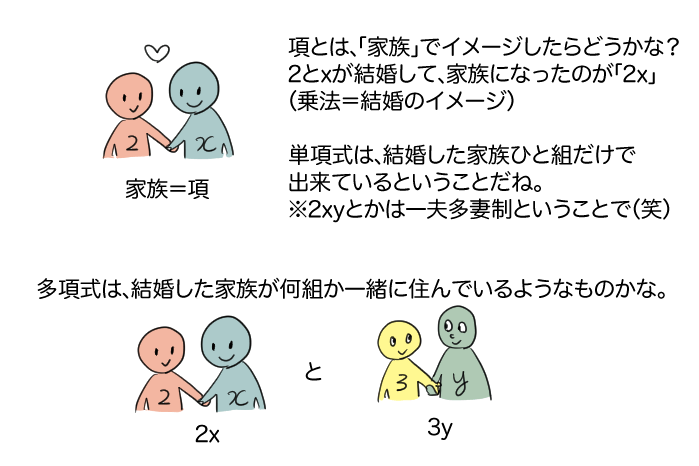
ちなみに、「\(2x\)」なども「ひとつの項」として考えるよ。
だって、\(2x\)とは、「2とxをかけたもの」という意味なだけだからね。
もちろん、\(2xy\)だって「2とxとyをかけたもの」だからひとつの項だよ。
「項」は中学1年生の数学で詳しく習っているよ。不安な場合は、中学1年数学のページを確認してね。
「項」が分かれば「単項式」と「多項式」のこともカンタン。
「単項式」というのは単(ひとつの)項で出来ている式のことだよ。
例:
\(2x\)
\(-7\)
厳密に言うと、「いくつかの数や文字をかけ合わせてできる式」なんだ。
(上の例の場合、2xは2とxをかけたもの、-7は-7と1をかけたもの、と考えるよ。)
言い換えると「乗法だけで出来ている式」だよ。なので、\(\frac{1}{x}\)は除法が混じってしまうから単項式ではないことに注意 。(分数式と言うよ)
\(\frac{1x}{2}\)のように、数字が分母になっている場合は大丈夫。
よ)
\(\frac{1}{2}\)と\(x\)の乗法と考えられるからね。\(\sqrt{x}\)のように、ルートの中に文字が入ってしまう場合も単項式ではなくなるよ。
※ややこしいけど、コレって結構テストに出たりするから要注意!
「多項式」は多(多数の)項で出来ている式のことだね。 2つ以上の項から出来ているよ。
例:
\(2x+3\)
(「\(2x\)」という項と、「\(+3\)」という2つの項で出来ている。)
単項式と多項式は中学2年の数学で登場するよ。不安な場合は確認しよう!
次数/多項式の次数とは・・
単項式に「x」とか「y」とかの文字が入っている場合、「入っている文字の数」を
その単項式の「次数」というよ。
例:
\(2x\) →xがひとつなので、次数は1。
\(2xy\) →xとyで2つの文字なので、次数は2
多項式の場合は、項が2つ以上あるから、それぞれの項に文字が入ってしまっていたら
なんだかややこしい話になるよね。
なので、多項式の次数は「一番たくさん文字が入っている項を代表」にするよ。
例:
\(2x^2+3y\) →「\(2x^2\)」は「xが2つ」なので次数は2。
「\(3y\)」は「yがひとつ」で次数は1。
「\(2x^2\)」のほうが次数が大きいから、こっちを代表にして、
この多項式の次数は「2」になる。
\(2x+3y^2+5xy^2\) →「\(5xy^2\)」が次数3で一番大きい。
この多項式の次数は「3」
次数も中学2年の数学で登場するよ。
係数とは・・
係数は、基本的には文字が含まれている項の、数の部分のことだよ。
※中学の数学までは数の部分という理解の仕方でいいけど、高校数学では
数の部分に限らないんだ。(この後説明が出てくるよ)
\(2x+3\)という式なら「文字が含まれる項」は\(2x\)だね。
「\(2x\)」の数は「2」だね。
なので、係数は「2」だよ。
\(2x+3y\)のように、文字が含まれる項がいくつかある場合は、
それぞれに係数があることになるよ。
上の式の場合、xの係数は2で、yの係数が3だよ。
「漢字検定8級を学習しよう!」で説明したとおり、
「係」は「つながり・関係ある」という意味があるんだ。
だから、xに「つながっている数字」だからxの係数、と覚えるといいね。

○○についての整式とは・・
定数項とは・・
単項式と多項式をまとめて「整式」と呼ぶんだ。
そしてこの「○○についての整式」という考え方が高校数学から初登場する。
「○○について」というのは、「○○に着目(注目)して!」という意味だよ。
「xについて」だったら「xに注目~!」ということでOK。
「○○について着目した場合、次数は」とか「○○について着目した場合、係数は」
なんていうふうに問題として登場してくるよ。
例:「○○についての着目した場合の次数の考え方」
\(2x^2+3y\)を「xについて着目した場合の次数」はxが入っている項のことで考えればいいよ。なので、次数はxという文字が2つで「2」だね。
「yに着目」したら、次数はyという文字がひとつだから「1」だね。
もし「xとy」に着目と言われたらどうなるかな?
xとyの次数を足したりしてはダメだよ。
あくまでxの入っている項と、yが入っている項に着目して、それぞれの次数を考えて、そのなかで一番大きい次数を答えなくてはいけないよ。
\(2x^2+3y\)の場合は、xの次数は2、yの次数は1、なので「xとy」に着目した場合は結局xの次数が一番大きいから「2」でいいんだ。
\(2x^2+3y+4z^3\)という式で「xとyについて着目」したらどうなるかな?
xとyが入っている項は、「\(2x^2\)」と、「\(3y\)」だね。この2つの項だけで次数を考えるから、結局一番大きいxの次数「2」でOK。
もちろん、「zについて着目」だったら次数は「3」だね。
問題文に「○○について着目」という言葉がない場合は、全部の文字について着目するよ。だから、「\(2x^2+3y+4z^3\)の次数は?」と聞かれた場合は、x・y・z全てに着目するから一番大きいzの次数「3」になるんだね。
そしてこの「○○について着目した場合」の係数の考え方が、ちょっと注意。
「係数は数字だけとは限らない」といった理由がコレなんだ。
例:「○○について着目したときの場合の係数の考え方」
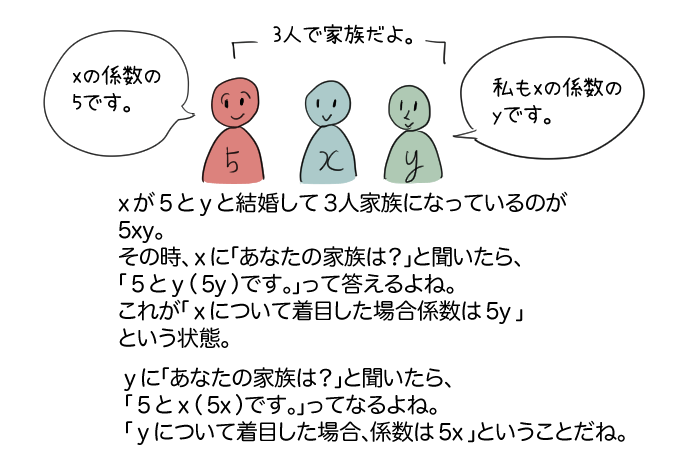
\(5x\)の係数は「5」
\(5xy\)の係数を、「xについて着目したとき」は「\(5y\)」になるよ。
係数は数字に限らないんだ。「xにつながっているもの」だからと考えれば、
納得だね。
いよいよ最後、
定数項とは「ある文字に着目したとき、その文字を含まない項」のこと だよ。
例えば「xに着目」したときなら、「xが入っていない項」のことだね。
例
\(2x+3y+4z\) を「xに着目したときの定数項」とは?
\(2x\)→xが入っている
\(3y\)、\(4z\)→xが入っていない
なので、定数項は「\(3y\)」と「\(4z\)」だね。
これは結構カンタンかな?
これで「式の整理」を学習するために必要な用語と知識はOK!
次は早速「整式の整理」について解説するよ!
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。






